oldja egyenletek numerikusan

keresse meg az összes gyökere egy polinom függvény

Use vpasolve hogy megtalálja az összes megoldást a funkció f(x)=6X7-2×6+3×3-8.

syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)

vpasolve a függvény hét gyökerét adja vissza a várt módon, mivel a függvény a hetedik fokozat polinomja.,

keresse meg a nem polinomiális függvény nulláit a keresési tartományok és a kiindulási pontok segítségével

az f(x)=e(x/7)cos(2x) függvény diagramja periodikus nullákat tár fel, a nulla pontokon növekvő lejtőkkel, ahogy x növekszik.

syms xh = fplot(exp(x/7)*cos(2*x),);grid on

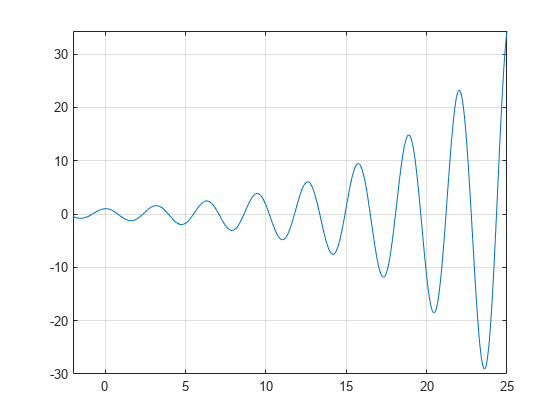
A vpasolve találni egy nulla a funkció f. Vegye figyelembe, hogy vpasolve egy nempolinom egyenlet egyetlen megoldását adja vissza, még akkor is, ha több megoldás létezik., On repeated calls, vpasolve returns the same result.

f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.

for k = 1:3 vpasolve(f,x,'Random',true)end

ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')

ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')

ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')

To find a zero close to x=10, set the starting point to 10.,

vpasolve(f,x,10)

ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')

ahhoz, Hogy megtalálja a nulla közeli x=1000, állítsa be a kiindulási pont, hogy a 1000.

vpasolve(f,x,1000)

ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')

ahhoz, Hogy megtalálja a nulla a tartomány 15≤x≤25, állítsa be a keresési tartományt .,

vpasolve(f,x,)

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ahhoz, Hogy megtalálja több nullát a tartomány , nem hívhatja vpasolve többször, mert vissza ugyanazt az eredményt minden hívás, mint a korábban bemutatott. Ehelyett állítsa be a keresési tartományt, majd állítsa a 'Random' értéket trueértékre.,

for k = 1:3 vpasolve(f,x,,'Random',true)end

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')

Mert 'Random' kiválasztja kiindulási pontok véletlenszerűen, ugyanaz a megoldás, lehet, hogy megtaláltuk egymást követő hívások.,

keresse meg az összes nullát egy megadott keresési tartományban

Hozzon létre egy függvényt findzeros hogy szisztematikusan megtalálja az összes nullát a f egy adott keresési tartományban, egy meghatározott hibatűrésen belül. A függvény A beviteli keresőtartományban kezdődik, és a vpasolve hívásokkal nullát keres. Ezután a keresési tartományt ketté osztja a nulla érték körül, majd rekurzív módon felhívja magát az új keresési tartományokkal bemenetként, hogy több nullát találjon.

a függvény magyarázata szakasz itt.,

deklarálja a függvényt A három bemenettel és egy kimenettel. Az első bemenet a függvény, a második bemenet a tartomány, az opcionális harmadik bemenet pedig lehetővé teszi a hiba megadását a nulla és az abból generált magasabb és alacsonyabb határok között.

function sol = findzeros(f,range,err)

ha nem adja meg a hibatűrés opcionális érvét, findzeroserr0.001.

if nargin < 2 err = 1e-3;end

Keressen egy nullát a keresési tartományban a vpasolvehasználatával.,

sol = vpasolve(f,range);

Ha vpasolve nem talál nullát, kilép.

if(isempty(sol)) return

If vpasolve nullát talál, a keresési tartományt két Keresési tartományra osztja a nulla felett és alatt.

else lowLimit = sol-err; highLimit = sol+err;

Call findzeros az alacsonyabb keresési tartomány. Ha afindzeros visszaadja a nullákat, másolja az értékeket a megoldás tömbbe, majd rendezze azokat.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end

hívás findzeros a magasabb keresési tartomány., Ha afindzeros visszaadja a nullákat, másolja az értékeket a megoldás tömbbe, majd rendezze azokat.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend

a teljes függvény findzeros a következő. Mentse el ezt a funkciót findzeros.m az aktuális mappában.

syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'

tetszőleges pontosságú megoldások beszerzése

digits a vpasolveáltal visszaküldött megoldások pontosságának beállításához., Alapértelmezés szerint avpasolve 32 Jelentős Szám pontossággal adja vissza a megoldásokat.

f = exp(x/7)*cos(2*x);vpasolve(f)

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

A digits növeli a pontosságot 64 jelentős számok. A digits módosításakor ügyeljen arra, hogy mentse az aktuális értékét, hogy visszaállíthassa.,

digitsOld = digits;digits(64)vpasolve(f)

ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')

ezután változtassa meg a megoldások pontosságát 16 jelentős számra.

digits(16)

többváltozós egyenletek megoldása a keresési tartományok segítségével

vegye figyelembe a következő egyenletrendszert.

a 0≤x≤2.5 és 0≤x≤2.5 egyenletek diagramja azt mutatja, hogy a három felület két pontban metszi egymást., A cselekmény jobb megjelenítéséhez használja a értéket. A colormap értékek méretezéséhez használja a caxisértéket.

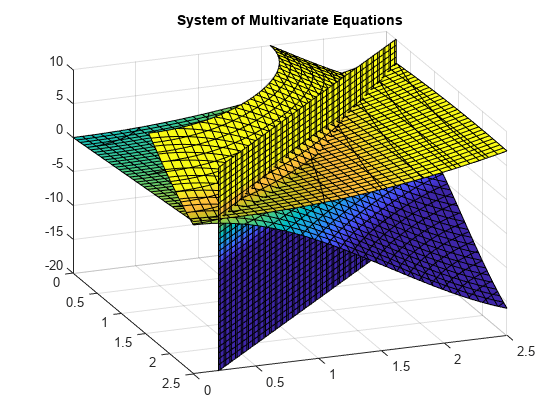
Usevpasolve egy pont megkereséséhez, ahol a felületek metszenek. A vpasolve függvény egy struktúrát ad vissza. A x-, y-, és z-a megoldás értékei, index a szerkezetbe.,

sol = vpasolve(equations);

a megoldási terület egy régiójának kereséséhez adja meg a változók Keresési tartományait. Ha a 0≤x≤1,5 és 1,5≤y≤2,5 tartományt adja meg, akkor avpasolve függvény megkeresi a megadott határolt területet.

használja avpasolve megoldást találni erre a keresési tartományra. A Z keresési tartomány kihagyásához állítsa a harmadik keresési tartományt értékre.,

vars = ;range = ;sol = vpasolve(equations, vars, range);

Több megoldás megtalálásához állítsa be a 'Random' opcióttrue. Ez teszi avpasolve véletlenszerű kiindulási pontokat az egymást követő futásokon. A'Random' opció használható a keresési tartományokkal együtt, hogy avpasolve véletlenszerű kiindulási pontokat használjon a keresési tartományon belül. Mivel a 'Random' véletlenszerűen választja ki a kiindulási pontokat, ugyanez a megoldás megtalálható az egymást követő hívásokon is., Hívja a vpasolve ismételten, hogy mindkét megoldást megtalálja.

rajzolja meg az egyenleteket. Helyezze a megoldásokat a sárga X jelölők scatter parcellájaként a scatter3használatával. A telek jobb megjelenítéséhez készítsen két felületet átlátszóvá a alphahasználatával. A színtérképet a caxis parcellaértékekre méretezzük, majd a perspektívát a viewsegítségével módosítjuk.

vpasolve megoldásokat talál az egyenletek által alkotott felületek metszéspontjában az ábrán látható módon.,

Lastly, restore the old value of digits for further calculations.

digits(digitsOld)