tartalom
állandó gyorsulás
mindannyian ismerjük azt a tényt, hogy egy autó felgyorsul, amikor a lábát a gázpedálra tesszük. A részecske sebességének időbeli változásának sebességét gyorsulásnak nevezik. Ha a részecske sebessége állandó sebességgel változik, akkor ezt az arányt állandó gyorsulásnak nevezik.,
például, ha egy egyenes vonalban mozgó részecske sebessége egyenletesen változik (állandó változási sebességgel) 2 m/s-ról 5 m/s-ra egy másodperc alatt, akkor állandó gyorsulása 3 m/s\(^2\).
csökkenő sebesség
Ha egy részecske kezdeti sebessége 6 m / s és állandó gyorsulása \(-2\) m/s\(^2\), akkor:
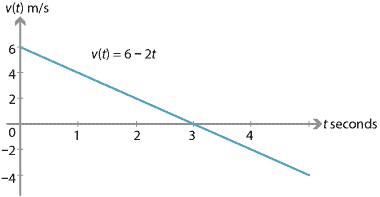
az első három másodpercben a részecske sebessége csökken (a részecske lassul). Három másodperc alatt a részecske pillanatnyilag nyugalomban van., Három másodperc múlva a sebesség még mindig csökken, de a sebesség növekszik (a részecske egyre gyorsabban megy).
összefoglaló
ha feltételezzük, hogy a sebességváltozás (gyorsulás) állandó, akkor az állandó gyorsulást
\
pontosabban az állandó gyorsulás \(a\) A
\
képlet adja meg, ahol \(v(t_i)\ (t_i\) az idő sebessége\(t_i\). Mivel a sebesség vektor, így a gyorsulás is.,
A mozgás állandó gyorsulási képletei egyenes vonalban
ebben a szakaszban az állandó gyorsulással egyenes vonalban gondolkodtunk. Ez a helyzet nagyon gyakori;például egy test, amely a gravitáció hatására mozog, állandó gyorsulással halad.
feltételezzük, hogy a mozgás akkor kezdődik, amikor \(t = 0\), és hogy a kezdeti pozíciót származásként veszik, azaz \(x(0) = 0\).,
Az öt egyenletek a mozgás
- \(v = u + a\)
- \(x = \dfrac{(u+v)t}{2}\)
- \(x = ut + \dfrac{1}{2}a^2\)
- \(v^2 = r^2 + 2ax\)
- \(x = vt – \dfrac{1}{2}a^2\)
Megjegyzés. Az öt egyenlet mindegyike az öt változóból négyet tartalmaz \(u,v, x, A, t\). Ha a változók közül három értéke ismert, akkor a fennmaradó értékek két egyenlet használatával találhatók meg.,
az állandó gyorsulási képletek
a mozgás első egyenlete
mivel a gyorsulás állandó, van \(a = \dfrac{v-u}{t}\). Ez adja a mozgás első egyenletét, \(v = u + at\).
a mozgás második egyenlete
a második egyenlet,
\
azt mondja, hogy az elmozdulást úgy kapjuk meg, hogy a kezdeti és végső sebesség átlagát megszorozzuk a mozgás során eltelt idővel. Egyszerűbben:
\
ezt az egyenletet abból a tényből tudjuk levezetni, hogy az elmozdulás megegyezik a sebesség–idő gráf alatt aláírt területtel.,
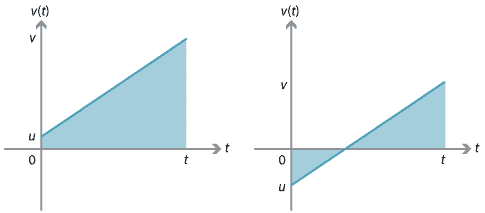
A jobb oldali grafikon esetében az elmozdulás a grafikon és a \(t\)-tengely közötti két háromszög figyelembevételével található meg. Az egyik háromszögnek pozitív aláírt területe van, a másiknak negatív aláírt területe van.
a részecske elmozdulását a sebesség–idő gráfból az integráció segítségével a modul egy későbbi szakaszában tárgyaljuk.,
a mozgás harmadik egyenlete
helyettesítve \(v\) az első egyenletből a második egyenletbe
\begin{align*}x &= \dfrac{(u+v)T}{2} \\ &= \dfrac{(u+u+at)T}{2} \\ &= \dfrac{2UT+at^2}{2} \\ &= ut + \dfrac{1}{2}at^2, \end{align*}
ami a harmadik egyenlet. Így a\ (x\) egy kvadratikus a \(t\) – ban, ezért a \(x\) \(t\) gráf egy parabola.
a mozgás negyedik egyenlete
az első egyenletből \(t = \dfrac{v-u}{a}\)., Ezt a második egyenletbe helyettesítve
\begin{align*}x &= \dfrac{(u+v)T}{2} \\ &= \dfrac{(u+v)(v-u)}{2A} \\ &= \dfrac{V^2-U^2}{2a}. \ end{align*}
átrendezve, hogy \ (v^2\) az alany a negyedik egyenletet hozza létre: \(v^2 = u^2 + 2AX\).
a mozgás ötödik egyenlete
az első egyenletből \(u = v-at\) van., A második egyenlet segítségével
\begin{align*}x &= \dfrac{(u+v)T}{2} \\ &= \dfrac{(v-at+v)T}{2} \\ &= \dfrac{2VT-at^2}{2} \\ &= VT-\dfrac{1}{2}at^2, \end{align*}
ami az ötödik egyenlet.
függőleges mozgás
a gravitáció miatti mozgás jó kontextus, amelyben az állandó gyorsulási képletek használatának bemutatására kerül sor., Mint arról korábban beszámoltunk, a két irány függőleges irányban felfelé és lefelé halad, és döntést kell hozni arról, hogy a két irány közül melyik pozitív. A gravitáció miatti gyorsulás állandó, a nagyságrendet \(g\) jelöli. A következő példában a felfelé mutató irányt vesszük pozitívnak, és \(g = 10\) m/s\(^2\) értéket vesszük.
3. gyakorlat
egy ember egy ugródeszkából merül, ahol súlypontja kezdetben 12 méterrel a víz felett van,kezdeti sebessége pedig 4,9 m/s felfelé., Tekintsd a búvár részecskének a súlypontjában, és tételezd fel, hogy a búvár mozgása függőleges.
- keresse meg a búvár sebességét \(t\) másodpercek után (egészen addig, amíg eléri a vizet).
- keresse meg a búvár magasságát a víz felett \(t\) másodpercek után (egészen addig, amíg eléri a vizet).
- keresse meg a búvár maximális magasságát a víz felett.
- keresse meg a búvár számára a víz eléréséhez szükséges időt.,
- vázolja fel ennek a mozgásnak a sebesség–idő grafikonját (egészen addig, amíg eléri a vizet).
- vázolja fel ennek a mozgásnak a pozíció–idő grafikonját (egészen addig, amíg eléri a vizet).
a mozgás egyenleteinek további használata
7. gyakorlat
egy autó 10 másodperc alatt 0 km/h-ról 100 km/h-ra gyorsul, és 40 másodpercig 100 km/h sebességgel folytatódik. a vezető ezután erősen fékez, hogy 38 méteren álljon meg.
- Konvertáljon 100 km/h-t m/s-ra.,
- keresse meg az autó állandó gyorsulását az első 10 másodpercben m/s\(^2\).
- keresse meg az autó által megtett teljes távolságot méterben.
- keresse meg a fékezési fázis gyorsulását m/s\ – ban(^2\).
- mennyi ideig tart az autó megállása, amikor a fékeket először alkalmazzák?
- vázoljon egy sebesség–idő grafikont az autó mozgásához.,
Next page – Content – Average velocity and average speed
 |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |