Inhalt-Konstante Beschleunigung

Inhalt

Konstante Beschleunigung

Wir alle kennen die Tatsache, dass ein Auto beschleunigt, wenn wir unseren Fuß auf das Gaspedal setzen. Die Änderungsrate der Geschwindigkeit eines Teilchens in Bezug auf die Zeit wird als Beschleunigung bezeichnet. Wenn sich die Geschwindigkeit des Teilchens mit konstanter Geschwindigkeit ändert, wird diese Geschwindigkeit als konstante Beschleunigung bezeichnet.,

Wenn sich beispielsweise die Geschwindigkeit eines Teilchens, das sich in einer geraden Linie bewegt, über eine Sekunde gleichmäßig (mit konstanter Änderungsrate) von 2 m/s auf 5 m/s ändert, beträgt seine konstante Beschleunigung 3 m/s\(^2\).

Geschwindigkeit verringern

Wenn ein Teilchen eine Anfangsgeschwindigkeit von 6 m/s und eine konstante Beschleunigung von \(-2\) m/s\(^2\) hat, dann:

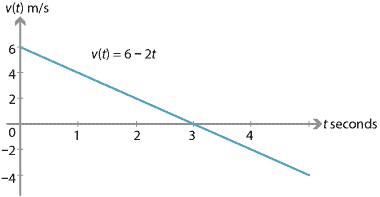
In den ersten drei Sekunden nimmt die Geschwindigkeit des Teilchens ab (das Teilchen verlangsamt sich). Nach drei Sekunden ist das Teilchen vorübergehend in Ruhe., Nach drei Sekunden nimmt die Geschwindigkeit immer noch ab, aber die Geschwindigkeit nimmt zu (das Teilchen wird immer schneller).

Zusammenfassung

Wenn wir annehmen, dass die Geschwindigkeit der Geschwindigkeitsänderung (Beschleunigung) eine Konstante ist, dann ist die konstante Beschleunigung gegeben durch

\

Genauer gesagt ist die konstante Beschleunigung \(a\) gegeben durch die Formel

\

wobei \(v(t_i)\) die Geschwindigkeit zur Zeit \(t_i\) ist. Da die Geschwindigkeit ein Vektor ist,ist auch die Beschleunigung.,

Die konstanten Beschleunigungsformeln für Bewegung in einer geraden Linie

In diesem Abschnitt haben wir Bewegung in einer geraden Linie mit konstanter Beschleunigung betrachtet. Diese Situation ist sehr häufig; Zum Beispiel bewegt sich ein Körper, der sich unter dem Einfluss der Schwerkraft bewegt, mit einer konstanten Beschleunigung.

Es wird angenommen, dass die Bewegung beginnt, wenn \(t = 0\), und dass die Ausgangsposition als Ursprung genommen wird, das heißt, \(x(0) = 0\).,

Die fünf Bewegungsgleichungen

1. \(v = u + at\)
2. \(x = \dfrac{(u+v)t}{2}\)
3. \(x = ut + \dfrac{1}{2}at^2\)
4. \(v^2 = u^2 + 2ax\)
5. \(x = vt – \dfrac{1}{2}at^2\)

Hinweis. Jede der fünf Gleichungen umfasst vier der fünf Variablen \(u, v, x, a, t\). Wenn die Werte von drei der Variablen bekannt sind, können die verbleibenden Werte mithilfe von zwei der Gleichungen gefunden werden.,

Ableitung der konstanten Beschleunigungsformeln

Die erste Bewegungsgleichung

Da die Beschleunigung konstant ist, haben wir \(a = \dfrac{v-u}{t}\). Dies ergibt die erste Bewegungsgleichung \(v = u + at\).

Die zweite Bewegungsgleichung

Die zweite Gleichung

\

besagt, dass die Verschiebung erhalten wird, indem der Durchschnitt der Anfangs-und Endgeschwindigkeit mit der Zeit multipliziert wird, die während der Bewegung verstrichen ist. Einfacher gesagt:

\

Wir können diese Gleichung daraus ableiten, dass die Verschiebung gleich der vorzeichenbehafteten Fläche unter dem Geschwindigkeitszeitdiagramm ist.,

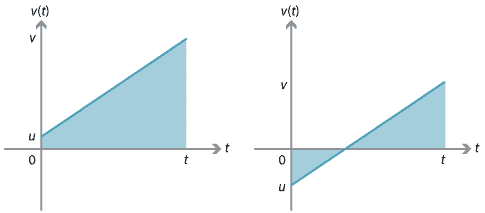
Für den Graphen auf der rechten Seite kann die Verschiebung unter Berücksichtigung der beiden Dreiecke zwischen dem Graphen und der \(t\)-Achse gefunden werden. Eines der Dreiecke hat einen positiv signierten Bereich und das andere einen negativ signierten Bereich.

Die Verschiebung eines Teilchens aus dem Geschwindigkeits–Zeit-Diagramm mithilfe der Integration zu finden, wird in einem späteren Abschnitt dieses Moduls diskutiert.,

Die Dritte Bewegungsgleichung

als Ersatz für \(v\) aus der ersten Gleichung in die zweite Gleichung gibt

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+in)t}{2} \\ &= \dfrac{2ut+an^2}{2} \\ &= ut + \dfrac{1}{2}bei^2, \end{align*}

das ist die Dritte Gleichung. Somit ist \(x\) ein quadratisches in \(t\), und daher ist der Graph von \(x\) gegen \(t\) eine Parabel.

Die vierte Bewegungsgleichung

Aus der ersten Gleichung haben wir \(t = \dfrac{v-u}{a}\)., Ersetzen Sie dies in die zweite Gleichung gibt

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-u^2}{2a}. \end{align*}

Neu Anordnen, um \(v^2\) Das Subjekt erzeugt die vierte Gleichung: \(v^2 = u^2 + 2ax\).

Die fünfte Bewegungsgleichung

Aus der ersten Gleichung haben wir \(u = v-at\)., Mit Hilfe der zweiten Gleichung, so erhalten wir

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-at+v)t}{2} \\ &= \dfrac{2vt-at^2}{2} \\ &= vt-\dfrac{1}{2}bei^2, \end{align*}

das ist die fünfte Gleichung.

Vertikale Bewegung

Bewegung aufgrund der Schwerkraft ist ein guter Kontext, in dem die Verwendung der konstanten Beschleunigungsformeln demonstriert werden kann., Wie bereits erwähnt, sind unsere beiden Richtungen in vertikaler Bewegung auf und ab, und es muss entschieden werden, welche der beiden Richtungen positiv ist. Die Beschleunigung aufgrund der Schwerkraft ist eine Konstante, deren Größe mit \(g\) bezeichnet wird. Im folgenden Beispiel nehmen wir die Aufwärtsrichtung positiv und nehmen \(g = 10\) m/s\(^2\).

Weitere Verwendung der Bewegungsgleichungen

Next page – Content – Average velocity and average speed