Finden Sie alle Wurzeln einer Polynomfunktion
Verwenden Sie vpasolve, um alle Lösungen für die Funktion f(x)=6×7-2×6+3×3-8 zu finden.
syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)
vpasolve gibt erwartungsgemäß sieben Wurzeln der Funktion zurück, da die Funktion ein Polynom des Grades sieben ist.,
Finden Sie Nullen einer nichtpolynomialen Funktion mithilfe von Suchbereichen und Startpunkten
Ein Diagramm der Funktion f(x)=e(x / 7)cos(2x) zeigt periodische Nullen mit zunehmenden Neigungen an den Nullpunkten, wenn x zunimmt.
syms xh = fplot(exp(x/7)*cos(2*x),);grid on
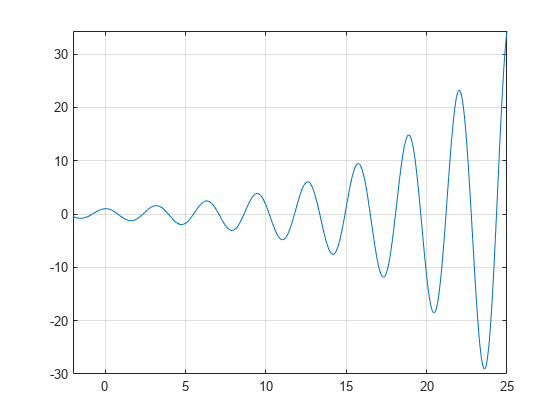
Verwenden Sie vpasolve, um eine Null der Funktion zu finden f. Beachten Sie, dass vpasolve nur eine Lösung einer nichtpolynomialen Gleichung zurückgibt, auch wenn mehrere Lösungen vorhanden sind., On repeated calls, vpasolve returns the same result.
f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.
for k = 1:3 vpasolve(f,x,'Random',true)end
ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')
ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')
ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')
To find a zero close to x=10, set the starting point to 10.,
vpasolve(f,x,10)
ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')
Um die Null nahe x=1000 zu finden, setzen Sie den Startpunkt auf 1000.
vpasolve(f,x,1000)
ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')
Um die Null im Bereich 15≤x≤25 zu finden, setzen Sie den Suchbereich auf .,
vpasolve(f,x,)
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
Um mehrere Nullen im Bereich zu finden, können Sie vpasolve
'Random' auf true.,
for k = 1:3 vpasolve(f,x,,'Random',true)end
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')
Da 'Random' Startpunkte zufällig auswählt, kann dieselbe Lösung bei aufeinanderfolgenden Aufrufen gefunden werden.,
Finden Sie alle Nullen in einem bestimmten Suchbereich
Erstellen Sie eine Funktion findzeros um systematisch alle Nullen für f in einem bestimmten Suchbereich innerhalb einer bestimmten Fehlertoleranz zu finden. Die Funktion beginnt mit dem Eingabesuchbereich und ruft vpasolve auf, um eine Null zu finden. Dann teilt es den Suchbereich um den Nullwert in zwei Teile auf und ruft sich rekursiv mit den neuen Suchbereichen als Eingaben auf, um weitere Nullen zu finden.
Die Funktion wird hier Abschnitt für Abschnitt erklärt.,
Deklarieren Sie die Funktion mit den drei Eingängen und einem Ausgang. Die erste Eingabe ist die Funktion, die zweite Eingabe ist der Bereich und mit der optionalen dritten Eingabe können Sie den Fehler zwischen einer Null und den daraus generierten höheren und niedrigeren Grenzen angeben.
function sol = findzeros(f,range,err)
Wenn Sie das optionale Argument für Fehlertoleranz nicht angeben, setzt findzeros err auf 0.001.
if nargin < 2 err = 1e-3;end
Suchen Sie eine Null im Suchbereich mit vpasolve.,
sol = vpasolve(f,range);
Wenn vpasolve nicht finden, eine null, beenden.
if(isempty(sol)) return
Wenn vpasolve eine Null findet, teilen Sie den Suchbereich in zwei Suchbereiche oberhalb und unterhalb der Null auf.
else lowLimit = sol-err; highLimit = sol+err;
Rufen Sie findzeros mit dem unteren Suchbereich auf. Wenn findzeros Nullen zurückgibt, kopieren Sie die Werte in das Lösungsarray und sortieren Sie sie.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end
Rufen Sie findzeros mit dem höheren Suchbereich auf., Wenn findzeros Nullen zurückgibt, kopieren Sie die Werte in das Lösungsarray und sortieren Sie sie.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend
Die gesamte Funktion findzeros ist wie folgt. Speichern Sie diese Funktion als findzeros.m im aktuellen Ordner.
syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'
Erhalten Lösungen zu Beliebige Präzision
Verwenden digits zu set die präzision der lösungen zurückgegeben durch vpasolve., Standardmäßig gibt vpasolve Lösungen mit einer Genauigkeit von 32 signifikanten Zahlen zurück.
f = exp(x/7)*cos(2*x);vpasolve(f)
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
Verwenden Sie digits, um die Genauigkeit auf 64 signifikante Zahlen zu erhöhen. Stellen Sie beim Ändern von digits sicher, dass Sie den aktuellen Wert speichern, damit Sie ihn wiederherstellen können.,
digitsOld = digits;digits(64)vpasolve(f)
ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')
als Nächstes ändern Sie die Genauigkeit der Lösungen zu 16 bedeutender Persönlichkeiten.
digits(16)
Lösen Sie multivariate Gleichungen mit Suchbereichen
Betrachten Sie das folgende Gleichungssystem.
z=10(cos(x)+cos (y))z=x+y2-0.1x2y-2.7=0
Ein Diagramm der Gleichungen für 0≤x≤2.5 und 0≤x≤2.5 zeigt, dass sich die drei Flächen in zwei Punkten schneiden., Um das Diagramm besser zu visualisieren, verwenden Sie view. Verwenden Sie zum Skalieren der Colormap-Werte caxis.
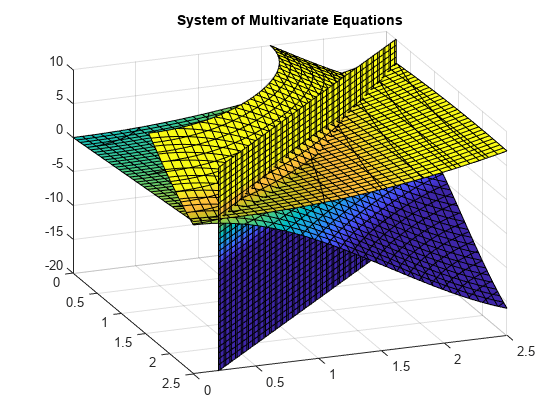
Verwenden Sie vpasolve, um einen Punkt zu finden, an dem sich die Oberflächen schneiden. Die Funktion vpasolve gibt eine Struktur. Um auf die x-, y – und z-Werte der Lösung zuzugreifen, indizieren Sie die Struktur.,
sol = vpasolve(equations);
Um einen Bereich des Lösungsraums zu durchsuchen, geben Sie Suchbereiche für die Variablen an. Wenn Sie die Bereiche 0≤x≤1,5 und 1,5≤y≤2,5 angeben, durchsucht die Funktion vpasolve den angezeigten begrenzten Bereich.

Verwenden Sie vpasolve, um eine Lösung für diesen Suchbereich zu finden. Um einen Suchbereich für z wegzulassen, setzen Sie den dritten Suchbereich auf .,
vars = ;range = ;sol = vpasolve(equations, vars, range);
Um mehrere Lösungen zu finden, setzen Sie die Option 'Random' auf true. Dadurch verwendet vpasolve zufällige Startpunkte bei aufeinanderfolgenden Läufen. Die Option 'Random' kann in Verbindung mit Suchbereichen verwendet werden, um vpasolve zufällige Startpunkte innerhalb eines Suchbereichs zu verwenden. Da 'Random' Startpunkte zufällig auswählt, kann bei aufeinanderfolgenden Aufrufen dieselbe Lösung gefunden werden., Rufen Sie vpasolve wiederholt auf, um sicherzustellen, dass Sie beide Lösungen finden.
Zeichnen Sie die Gleichungen. Überlagern Sie die Lösungen als Streudiagramm von Punkten mit gelbenX Markern mit scatter3. Um das Diagramm besser zu visualisieren, machen Sie zwei der Oberflächen mit alphatransparent. Skalieren Sie die Farbkarte mit caxis auf die Plotwerte und ändern Sie die Perspektive mit view.
vpasolve findet Lösungen am Schnittpunkt der durch die Gleichungen gebildeten Flächen wie gezeigt.,

Lastly, restore the old value of digits for further calculations.
digits(digitsOld)