Auf diesen Seiten betrachten wir einige interessante Konzepte, wir betrachten gekrümmten Raum: Was gekrümmter Raum bedeutet, wie wir sagen können, ob ein Raum von innen oder von außen gekrümmt ist.
Wir schauen uns an, wie wir nach Art des Raums in einen anderen einbetten können, und sehen, dass wir zwischen verschiedenen Räumen auf unterschiedliche Weise zuordnen können.
Wir betrachten auch die Verdichtung und wie wir unendlich große und unendlich kleine Vektoren in unseren Räumen auf eine Weise darstellen können, die nicht zu Singularitäten und anderen Problemen führt.,
Diese Konzepte erweisen sich als nützlich, selbst wenn wir mit flachem Raum arbeiten, werden wir Wege finden, Vektoren und Ebenen darzustellen, die den Ursprung nicht durchlaufen. Dies gibt uns Möglichkeiten, Rotationen und Übersetzungen als eine einzige Operation darzustellen.
Die andere Anwendung ist relativistische Raum-Zeit.
Rienmannsche Geometrie
In der Rienmannschen Geometrie kann sich der Raum an verschiedenen Stellen krümmen (siehe Manifolds) Hier betrachten wir Geometrien, bei denen die Raumkurve konstant ist.,
Eulidische Geometrie
flacher Raum
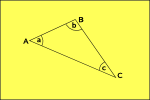
Hyperbolische Geometrie
Raumkurven nach außen
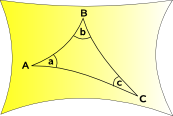
Sphärische Geometrie und elliptische Geometrie
Raumkurven nach innen
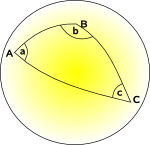
In einer gekrümmten (nicht-euklidischen) Geometrie können wir keinen Satz von Koordinaten finden, die zueinander senkrecht stehen, wobei die Koordinatenlinien alle parallel zueinander sind und wo jedes Gitterquadrat die gleiche Fläche hat., Möglicherweise finden wir ein Koordinatensystem, in dem wir einige davon ausführen können, aber nicht alle.
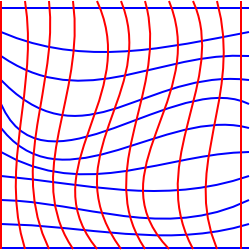
Dieses Diagramm versucht, diese Situation in 2 Dimensionen zu veranschaulichen, obwohl es etwas irreführend ist, weil wir es auf einer Ebene gezeichnet haben, damit wir rechteckige Koordinaten zeichnen können.
Um eine Situation zu veranschaulichen, in der dies unmöglich ist, könnten wir uns eine zweidimensionale Ebene vorstellen, die in die dritte Dimension gestreckt wurde.,

In dieser Situation können wir Koordinaten auswählen, die ein rechteckiges Gitter bilden, wenn es auf eine horizontale Ebene projiziert wird, jedoch auf eine Person, die in der Oberfläche lebt Dann scheinen einige der Gitterquadrate eine größere Fläche zu haben als andere und die Gitterlinien scheinen möglicherweise nicht parallel zu sein. Es gibt kein zweidimensionales Koordinatensystem, das parallele Linien, Winkel und Bereiche gleichzeitig beibehält.,
Ein ähnliches Beispiel versucht, die Erdoberfläche abzubilden, wir können Breiten-und Längenlinien verwenden, aber die Längenlinien nähern sich näher an den Polen.
In diesen Fällen könnten wir in Bezug auf dreidimensionale Koordinaten arbeiten, und das ist ein Ansatz, den wir mit einigen Arten von nicht-euklidischen Geometrien verfolgen werden. Es ist oft möglich, eine bestimmte Geometrie in eine höherdimensionale Geometrie einzubetten, um sie euklidischer zu gestalten.,
Manchmal ist es so, dass, wenn wir eine Geometrie in großem Maßstab betrachten, sie nicht euklidisch ist, aber wenn wir sie in immer kleinerem Maßstab betrachten, dann nähert sie sich einer euklidischen Geometrie an. Dazu müssen wir ein Koordinatensystem finden, in dem an jedem Punkt Winkel erhalten bleiben, dh die horizontalen und vertikalen Koordinatenlinien müssen sich immer bei 90° schneiden, obwohl die Linien möglicherweise nicht gerade sind. Dies wird als konforme Geometrie bezeichnet. In dieser Art von Geometrie können wir zumindest ein lokales Koordinatensystem definieren.,
Damit verbunden ist, ob die Geometrie differenziert und integriert werden kann, Voraussetzung dafür ist, dass sie sich gut benehmen muss und keine plötzlichen Sprünge etc. aufweist. Einige Geometrien und Koordinatensysteme können sich an einigen Stellen gut verhalten, haben aber Singularitäten usw.
Informationen zur Messung der Krümmung finden Sie auf dieser Seite.
Mathematische Notation
Wie gehen wir mit Geometrien um, bei denen wir nicht alle Regeln verwenden können, die für die euklidische Geometrie gelten?,
Ein Ansatz ist die Verwendung der Tensor-Notation, dies bietet Konventionen und Notation, die uns beim Umschalten zwischen verschiedenen Koordinatensystemen helfen. Ein orthogonales Koordinatensystem, das an einem beliebigen Punkt lokalisiert ist, kann mithilfe von Basisvektoren definiert werden, die Tangenten zu den Koordinatenlinien sind.,Manifold
siehe diese Seite
Beziehung zwischen hyperbolischen und Minkowski-Geometrien
| Minkowski-Geometrie | Hyperbolische Geometrie | |
| Punkt | Ereignis in der Raumzeit | Partikel in gleichmäßiger Bewegung |
| Abstand zwischen zwei Punkten | Raum-Zeit-Abstand zwischen zwei Ereignissen | relative Geschwindigkeit zwischen zwei solchen Teilchen |
Terminologie
Hier betrachten wir die Terminologie wie Geometrien, Räume, Modelle, Projektionen und Transformationen., Es ist ziemlich schwierig, wenn wir uns mit nicht-euklidischen Geometrien befassen, da wir eine ähnliche Terminologie verwenden, die wir im herkömmlichen euklidischen Raum gewohnt sind, aber die Begriffe können leicht unterschiedliche Eigenschaften haben.,versuchen
Elliptische Geometrie
Modelle
Beispiele sind:
- Oberen halb-ebene modell
- Poincare disc modell
- Projektives Modell
- Konformes Modell
Projektionen
Stereographische Projektion
Transformationen
Invariante
Beispiele sind:
- Möbius-Transformation
- Lorentz-Transformation
Parallel-Postulat
Wenn wir das parallele Postulat von der Euklidischer Raum.,
Dies führt zu:
- paralleles Postulat ist falsch
- Die Winkel eines Dreiecks addieren sich nicht zu π
- für eine Form einer bestimmten Größe gibt es im Allgemeinen keine ähnliche Form einer größeren Größe.,ctive
konform (Poincaré disc ) gerade Linien – Geodäsie Segmente von Kreisen Winkel ehr Innenwinkel des Dreiecks π-(α+β+γ)=CΔ Abstand zwischen zwei Punkten mit