Moore and Mealy Machines (Deutsch)

Output State Output → a b x1 c x1 b b x2 d x3 c d x3 c x1 d d x3 d x2

The state diagram of the above Mealy Machine is −

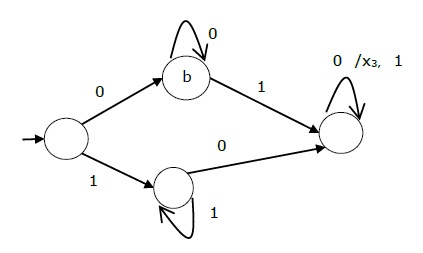
Moore Machine

Moore machine is an FSM whose outputs depend on only the present state.,

Eine Moore-Maschine kann durch ein 6 −Tupel (Q, ∑, O, δ, X, q0) beschrieben werden, wobei –

• Q eine endliche Menge von Zuständen ist.

• ∑ ist eine endliche Menge von Symbolen, die als Eingabealphabet bezeichnet werden.

• O ist eine endliche Menge von Symbolen, die als Ausgabealphabet bezeichnet werden.

• δ ist die Eingangsübergangsfunktion, wobei δ: Q × ∑ → Q

• X die Ausgangsübergangsfunktion ist, wobei X: Q → O

• q0 der Ausgangszustand ist, von dem aus eine Eingabe verarbeitet wird (q0 ∈ Q).,iv>

  Present state Next State Output Input = 0 Input = 1 → a b c x2 b b d x1 c c d x2 d d d x3

  The state diagram of the above Moore Machine is −

  

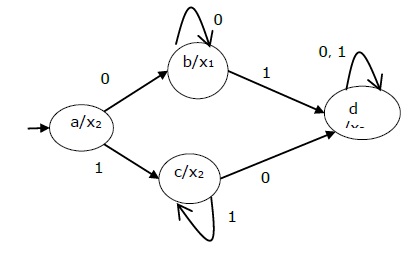
  Mealy Machine vs., Moore-Maschine

  Die folgende Tabelle hebt die Punkte hervor, die eine mehlige Maschine von einer Moore-Maschine unterscheiden.

  Mehlige Maschine	Mehlige Maschine
  Die Ausgabe hängt sowohl vom gegenwärtigen Zustand als auch vom gegenwärtigen Zustand ab	Die Ausgabe hängt nur vom gegenwärtigen Zustand ab.
  Im Allgemeinen hat es weniger Zustände als die Maschine.	Im Allgemeinen hat es mehr Zustände als mehlige Maschine.,
  Der Wert der Ausgabefunktion ist eine Funktion der Übergänge und der Änderungen, wenn die Eingabelogik für den aktuellen Zustand abgeschlossen ist.	Der Wert der Ausgabefunktion ist eine Funktion des aktuellen Zustands und der Änderungen an den Takträndern, wenn Zustandsänderungen auftreten.
  Mehlige Maschinen reagieren schneller auf Eingaben. Sie reagieren im Allgemeinen im selben Taktzyklus.	In Moore-Maschinen ist mehr Logik erforderlich, um die Ausgänge zu dekodieren, was zu mehr Schaltungsverzögerungen führt. Sie reagieren in der Regel einen Taktzyklus später.,

  Moore Maschine zu Mehlig Maschine

  Algorithmus 4

  Input − Moore Maschine

  Output − Mehlig Maschine

  Schritt 1 − Nehmen eine leere Mehlig Maschine übergang tabelle format.

  Schritt 2-Kopieren Sie alle Moore Machine-Übergangszustände in dieses Tabellenformat.

  Schritt 3-Überprüfen Sie die gegenwärtigen Zustände und ihre entsprechenden Ausgänge in der Tabelle des Maschinenstatus Moore; Wenn für einen Zustand der Qi-Ausgang m ist, kopieren Sie ihn in die Ausgabespalten der mehligen Maschinenstatus-Tabelle, wo immer Qi im nächsten Zustand erscheint.,der the following Moore machine −

  Present State	Next State		Output
  	a = 0	a = 1
  → a	d	b	1
  b	a	d	0
  c	c	c	0
  d	b	a	1

  Now we apply Algorithm 4 to convert it to Mealy Machine.,8″>