La oss begynne med et enkelt eksempel, la oss si vi ønsker å multiplisere ut (2x-3)3. Dette ville ikke være for vanskelig å gjøre for lenge siden, men la oss bruke den binomiske teorem, slik at når du støter på større utvidelser som binomials hevet til 4, 5, 6, … krefter, vet du nøyaktig hva du skal gjøre.
for Å komme i gang, du trenger for å identifisere de to begrepene fra binomial (x-og y-stillinger på vår formelen ovenfor) og kraft (n) du er å utvide den binomiske til.,
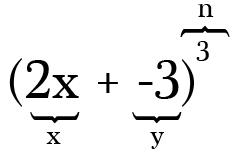
For eksempel, for å utvide (2x-3)3, de to begrepene 2x og -3 og makt, eller n-verdi, er 3. Merk at når du har en subtraksjon i binomial det er akk så viktig å huske å inkludere minus som et negativt symbol på den medfølgende sikt.
Den fantastiske ting om binomiske teorem er det tillater oss å finne utvidede polynom uten å multiplisere en haug av binomials sammen. Ganske kult, ikke sant?, Det viser seg at antall vilkårene i din utvidet polynom vil alltid være én mer enn den makt du er voksende. Det betyr at vi vil være å skape et polynom med 4 vilkår siden strømmen i dette eksemplet er 3.
Hver termin vil ha en (2x) og (-3) samt «n velge k» formel der n=3. Du kan gå fram og skriv det ned 4 ganger, en for hver termin, forlater k-verdien i «n velge k» og krefter tomt for øyeblikket.
Neste du ønsker å fylle i k-verdier og krefter. Her kan du følge summering formel, øke effekten for hver termin., Men det er ganske lett å bare følge mønstre.
k-verdier i «n velge k», starter med k=0, og øke med 1 i hver termin. Det siste begrepet bør ende med n lik k, i dette tilfellet n=3 og k=3.
Neste vi trenger å legge krefter inn (2x) og (-3).
The power on (2x) vil begynne med n-verdi, så i dette tilfellet 3, og vil reduseres med 1 på hver termin, til du kommer til null. Strømmen på (-3) vil starte med null og økes med en for hver gang til du kommer til n, eller 3 i dette problemet.,

Fordi noen verdi hevet til null strøm er lik 1, kan du forenkle vilkårene med krefter på null.

Neste gå foran og bruke krefter og forenkle der det er mulig.,

Pascal ‘ s Trekant Snarvei

Den siste delen er å løse kombinasjoner formel. Den åpenbare måten å gjøre dette på er å bruke kombinasjoner formel for hvert problem. Men vi kommer til å ta en fin liten snarvei her ved hjelp av Pascal ‘ s Trekant.
Pascal ‘ s Trekant er en enkel, men kraftig triangelet som, formes ved å lage en trekant med tre 1 å begynne., For hver rad du da bare skrive 1 på begge ender, og finn midten tall(e) ved å legge til de to verdiene fra rett ovenfor.

her er den gode del. Skjult i Pascal ‘ s Trekant er alle svarene til noen «n velge k»! Det er som en hemmelig liten cheatsheet!
diagrammet nedenfor viser hvor du skjult «n velge k s» er plassert.,

For vårt problem vi må løse for: 3 velg 0, 3 velg 1, 3 velg 2 og 3 for å velge 3. Der er alle verdiene i 4. rad. Så alt vi trenger å gjøre er å se til 4. rad av Pascal ‘ s Trekant og matche opp svarene.
4. rad har verdiene: 1, 3, 3, 1. Så jeg vil bare erstatning i løsninger for våre n velge k s.,

til Slutt, alt du trenger å gjøre er å multiplisere og forenkle hvert semester skal ned til er det enkleste form. Ikke glem å sjekke det endelige svaret å sørge for at krefter på hver termin fortsatt legge til graden av din opprinnelige binomiske! Stol på meg, det er utrolig enkelt å lage en transkripsjon feil i denne type problem 😉
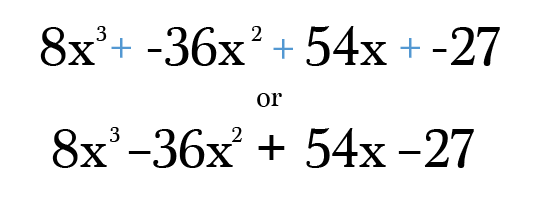
Trenger et annet eksempel?,
I videoen ovenfor, skal jeg vise deg hvordan du bruker den Binomiske Teorem å utvide binomial (x – 3y)også søke. Pluss jeg vise deg noen flere triks for å holde orden og et par raske sjekker du kan bruke til enkelt å identifisere vanlige feil.
Takk for at du leser!
❤ HOLDE kontakten ❤
du vil Holde deg oppdatert med alt Matematikk Hacks er opp til!