– >

Den Dirac delta funksjon er en funksjon som ble introdusert i 1930 av P. A. M. Dirac i sin banebrytende bok på kvantemekanikk. En fysisk modell som visualiserer en delta-funksjonen er en massedistribusjon av endelig total masse M—integralet over massedistribusjon., Når fordelingen blir mindre og mindre, mens M er konstant, massedistribusjon krymper til et punkt masse, som per definisjon har null grad, og ennå har begrenset verdsettes integrert lik total masse M. I grensen av et punkt masse fordelingen blir en Dirac delta-funksjonen.
Heuristically, den Dirac delta-funksjonen kan sees som en forlengelse av Kronecker deltaet fra integrert indekser (elementer av 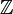 ) til ekte indekser (elementer av
) til ekte indekser (elementer av 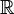 )., Vær oppmerksom på at Kronecker delta fungerer som et «filter» i en summering:
)., Vær oppmerksom på at Kronecker delta fungerer som et «filter» i en summering:
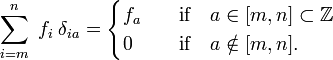
I analogi, den Dirac delta funksjon δ(x−a) er definert ved (erstatt jeg av x og summering over jeg ved en integrasjon over x),
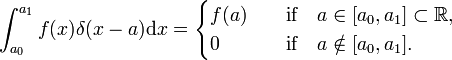
Den Dirac delta-funksjonen er ikke en vanlig veloppdragen kart  , men en fordeling, også kjent som en feil eller generalisert funksjon. Fysikere uttrykke sin spesielle karakter ved å si at Dirac delta-funksjonen gjør bare mening som en faktor i en integrand («under integrert»)., Matematikere si at delta-funksjonen er en lineær funksjonelle på en plass av test funksjoner.
, men en fordeling, også kjent som en feil eller generalisert funksjon. Fysikere uttrykke sin spesielle karakter ved å si at Dirac delta-funksjonen gjør bare mening som en faktor i en integrand («under integrert»)., Matematikere si at delta-funksjonen er en lineær funksjonelle på en plass av test funksjoner.
Innhold
- 1 Egenskaper
- 2-Deltaet-konvergerende sekvenser
- 2.1 Blokkere funksjoner
- 2.2 Gauss funksjoner
- 2.3 Lorentz-Cauchy funksjoner
- 2.4 Sinc funksjoner
- 3 Derivater av delta-funksjonen
- 3.,1 Egenskaper for derivat
- 4 Primitive
- 5 Dirac delta funksjon i tre dimensjoner
- 6 Referanser
Egenskaper
vanligvis tar man den nedre og øvre grense i definisjonen av delta-funksjonen lik 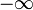 og
og 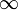 , henholdsvis. Herfra på dette vil bli gjort.
, henholdsvis. Herfra på dette vil bli gjort.
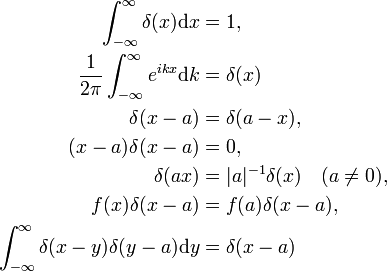
fysikeren er bevis av disse egenskapene innbetalinger ved å gjøre riktig innbytter i integrert og ved hjelp av de vanlige reglene for integrert kalkulus., Delta fungere som en Fourier transform av enheten funksjonen f(x) = 1 (annen eiendom), vil bli vist nedenfor. Den siste egenskapen er analogien av multiplikasjon av to identitet matriser,
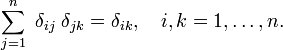
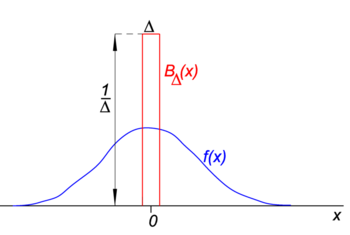
Fig. 1. Blokk («boxcar») funksjon (red) ganger vanlig funksjon f(x) (blå).
Delta-konvergerende sekvenser
Det finnes familier av vanlige funksjoner Fa(x) som familiemedlemmer forskjellige ved verdien av en enkelt parameter α., Et eksempel på en slik familie er dannet av familien av Gaussiske funksjoner Fa(x) = exp(−ax2), hvor ulike verdier av enkelt parameter α skille mellom de ulike medlemmene. Når alle medlemmene er lineært normalizable, dvs., følgende integral er endelig uavhengig av α,
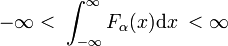
og alle medlemmer topp rundt x = 0, så familien kan danne en delta-konvergerende rekkefølge.,
Blokkere funksjoner
Den enkleste eksempel på en delta-konvergerende sekvensen er dannet av familien blokkere funksjoner, preget av positive Δ,
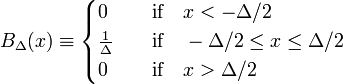
I Fig. 1 blokk funksjonen BΔ er vist i rødt. Tydeligvis, området (bredde ganger høyde) under den røde kurven er lik enhet, uavhengig av verdien av Δ,
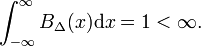
La vilkårlig funksjon f(x) (blå i Fig. 1) være kontinuerlig (uten hopp) og endelig i nabolaget til x=0., Når Δ blir veldig små, og blokkere funksjonen veldig smal (og nødvendigvis veldig høy fordi bredde ganger høyde er konstant) produktet f(x) BΔ(x) blir i god tilnærming lik f(0) BΔ(x). Den smalere blokkere bedre tilnærming., Dermed Δ kommer til null,
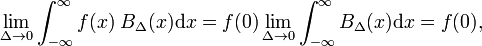
som kan sammenlignes med den definisjon av delta-funksjonen,
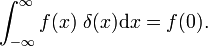
Dette viser at familien blokkere funksjoner konvergerer til Dirac delta-funksjonen for å redusere parameter Δ; familien danner et delta-konvergerende rekkefølge:
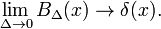
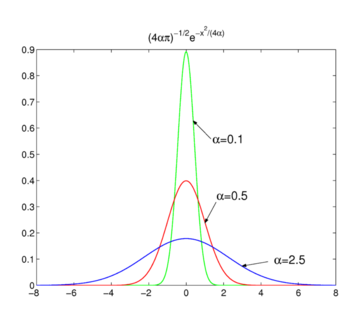
Fig. 2. Gaussian funksjoner.
Merk: Vi har integrert over hele den reelle aksen., Dette er åpenbart ikke nødvendig, vi kunne ha utelukket null-verdi vinger av blokker funksjon, og integrert bare over kneika i midten, fra −Δ/2 +Δ/2. I matematiske tekster, som for eksempel Ref. dette raffinement i integrering grenser er inkludert i definisjonen av delta-konvergerende rekkefølge. Det vil si at det er nødvendig at integraler over to vinger forsvinne i grensen. Fordi delta-konvergerende sekvenser som er oppstått i fysisk programmer vanligvis tilfredsstille denne tilstanden, vi utelater mer presis matematisk definisjon.,
Gaussian funksjoner
Tenk familien,
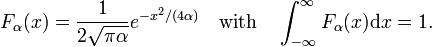
Som er vist i Fig. 2 funksjoner topp rundt x = 0 og bli smalere for å redusere α. Derav familie av Gaussiske funksjoner danner et delta-konvergerende sekvens,
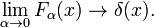
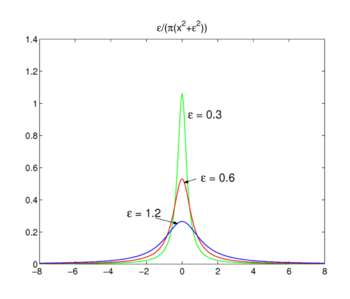
Fig. 3. Lorentz-Cauchy funksjoner
Lorentz-Cauchy funksjoner
familien av funksjonene som vises i Fig., 3
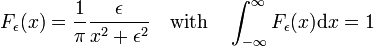
forms a delta-convergent sequence,
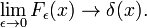
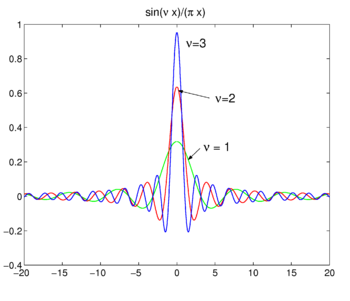
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 er
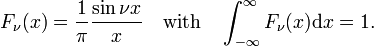
Denne familien konvergerer til å delta-funksjonen for å øke ν
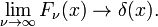
Denne grensen fører lett til Fourier-integral representasjon av delta-funksjonen:
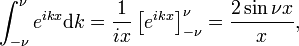
slik at
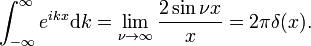
Den Dirac delta-funksjonen er Fourier-transform av enheten funksjonen f(x) = 1.
Derivater av delta funksjon
Vurdere en differensiable funksjonen f(x) som forsvinner på pluss og minus uendelig.,d=»ed7dae11d6″>
På samme måte som man beviser omsetning regel og Hermiticity av den kvantemekaniske momentum operatør 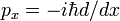 vi viste her at d/dx er anti-Hermitian,
vi viste her at d/dx er anti-Hermitian,
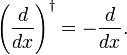
Faktisk, når vi skriver integrert som en indre produkt, det følger av delvis integrasjon og bortfallet av f(x) på integrering grenser som
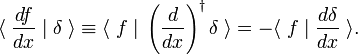
Denne omsetningen regel er brukt som definisjon av den deriverte av delta-funksjonen,
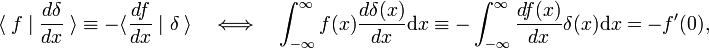
hvor prime angir den første deriverte av f(x)., I henhold til definisjonen av delta-funksjonen er den første deriverte er evaluert i x = 0. Ved hjelp av m ganger omsetningen regel følger det at mth derivat av delta-funksjonen er definert ved
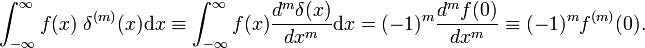
Egenskaper av derivatet
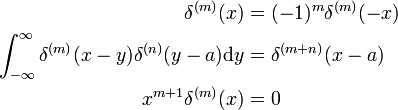
Disse resultatene kan bevises ved å gjøre erstatningen x → −x og bruk av omsetningen regel for d/dx (se ovenfor).,
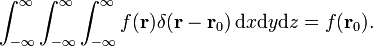
De tre-dimensjonale delta-funksjonen kan være factorized
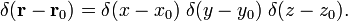
I sfæriske polare koordinater
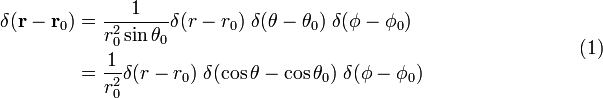
Bevis av ligning (1)
Skriv
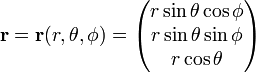
Jacobian (Jacobi determinant) denne transformasjonen fra Kartesiske sfæriske koordinater til polare koordinater er
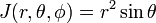
Tenk
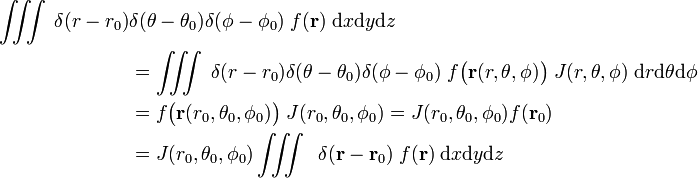
slik at
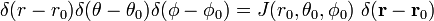
og
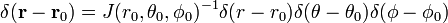
Den siste linjen i ligning (1) følger fra kjeden regelen.,
følgende nyttig og ofte brukt eiendommen er vist her,
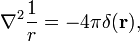
hvor ∇2 er Laplace-operatoren i tre-dimensjonale Kartesiske koordinater og r er lengden av r.