Logaritmiske funksjoner er inverses av den eksponentielle funksjoner. Den inverse av den eksponentielle funksjonen y = ax, x = ay. Den logaritmiske funksjonen y = logax er definert til å være tilsvarende den eksponentielle ligningen x = ay. y = logax bare under følgende forhold: x = ay, en > 0, og en≠1. Det kalles den logaritmiske funksjonen med base-en.
Tenk på hva den inverse av den eksponentielle funksjonen innebærer: x = ay., Gitt et tall x og en base, å hvilken kraft y må en være hevet til lik x? Denne ukjente eksponent, y, lik logax. Så du ser en logaritmen er ingenting mer enn en eksponent. Ved definisjon, alogax = x for alle reelle x > 0.
Nedenfor er avbildet grafer av formen y = logax når en > 1 og 0 < en < 1. Legg merke til at domenet består bare av positive reelle tall, og at funksjonen alltid øker når x øker.,
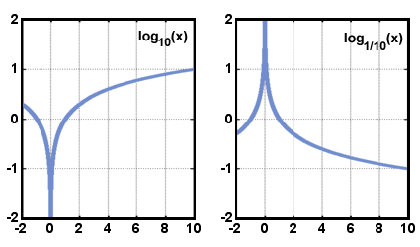
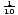 x.
x.domenet til en logaritmisk funksjon er reelle tall større enn null, og utvalget er reelle tall. Grafen til y = logax er symmetrisk til grafen til y = ax med hensyn til linjen y = x. Dette forholdet er sant for en hvilken som helst funksjon og dens inverse.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(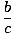 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
En naturlig logaritmisk funksjon er en logaritmisk funksjon med base e. f (x) = logex = ln x, hvor x > 0. ln x er bare en ny form for notasjon for logaritmer med base e. De fleste kalkulatorer har knappene merket «logg» og «ln». Den «logg» – knappen forutsetter basen er ti, og «ln» – knappen, selvfølgelig, lar base lik e., Den logaritmiske funksjonen med base 10 er noen ganger kalt felles logaritmisk funksjon. Det er brukt mye på grunn vår nummerering systemet har base ti. Naturlige logaritmer er sett oftere i kalkulus.
To formler eksisterer som tillater foten av en logaritmisk funksjon endres. Den første som sier dette: logab = 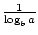 . De mer berømte og nyttig formel for å endre baser er ofte kalt Endring av Base Formel. Det gjør at bunnen av en logaritmisk funksjon for å bli endret til noe positivt reelt tall ≠1. Den sier at logax =
. De mer berømte og nyttig formel for å endre baser er ofte kalt Endring av Base Formel. Det gjør at bunnen av en logaritmisk funksjon for å bli endret til noe positivt reelt tall ≠1. Den sier at logax = 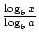 ., I dette tilfellet, a, b og x er alle positive reelle tall og a, b≠1.
., I dette tilfellet, a, b og x er alle positive reelle tall og a, b≠1.
I den neste seksjonen vil vi diskutere noen anvendelser av eksponential-og logaritmefunksjoner.