«enhetssirkelen» er en sirkel med en radius på 1.
å Være så enkelt, det er en flott måte å lære og snakke om lengder og vinkler.
The center er satt på en graf der x-aksen og y-aksen korset, så vi får denne ryddig arrangement her.
Sinus, Cosinus og Tangens
Fordi radius er 1, kan vi direkte måle sinus, cosinus og tangens.,
Hva skjer når vinkelen, θ, 0°?
cos 0° = 1, synd 0° = 0 og tan 0° = 0
Hva skjer når θ er 90°?
cos 90° = 0, synd 90° = 1 og tan 90° er udefinert
Prøv Det Selv!
Ha en prøve!, Flytte musen rundt for å se hvordan de forskjellige vinkler (i radianer eller grader) påvirker sinus, cosinus og tangens
«sider» kan være positive eller negative i henhold til reglene i Kartesiske koordinater. Dette gjør sinus, cosinus og tangens veksle mellom positive og negative verdier også.
prøv Også den Interaktive Enheten Sirkelen.,
Pytagoras
Pythagoras’ Teorem sier at for en rettvinklet trekant, kvadrat av den lange siden er lik summen av kvadratene på de to andre sidene:
x2 + y2 = 12
Men 12 er bare 1, slik:
x2 + y2 = 1
(ligning av enhetssirkelen)
Også, siden x=cos og y=sin, får vi:
(cos(θ))2 + (sin(θ))2 = 1
en nyttig «identitet»
Viktig Vinkler: 30°, 45° og 60°
Du bør prøve å huske sin, cos og tan for vinkler 30°, 45° og 60°.,
Ja, ja, det er en smerte å ha til å huske ting, men det vil gjøre livet enklere når du vet dem, ikke bare i eksamen, men andre ganger når du trenger å gjøre raske estimater, etc.
Dette er de verdiene du bør huske på!,id=»0f47f3223b»>
What about tan?,
Vel, tan = sin/cos, så kan vi beregne det som dette:
tan(30°) =sin(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sin(45°)cos(45°) = √2/2√2/2 = 1
tan(60°) =sin(60°)cos(60°) = √3/21/2 = √3
* Merk: du skriver 1√3 kan koste deg merker (se Rasjonell Denominators), så i stedet bruke √33
Rask Skisse
en Annen måte å hjelpe deg å huske 30° og 60° er å gjøre en rask skisse:
| Tegne en trekant med side lengder av 2 | 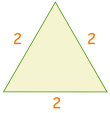 |
|
|
halvert.,div id=»56c966b492″> Eksempel: sin(30°)Sinus: sohcahtoa sinus er motsatt delt av hypotenuse
sin(30°) = oppositehypotenuse = 12
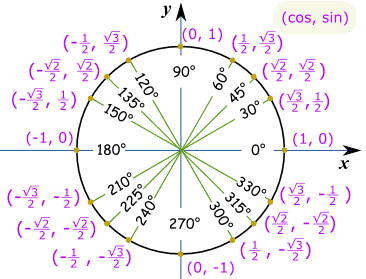
Hele SirkelFor hele sirkelen vi må verdiene i hver kvadrant, med riktig pluss-eller minustegn som per Kartesiske Koordinater: Merk at cos er først og synd er det andre, så det går (cos, synd):
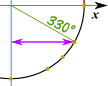
Lagre som PDF – Eksempel: Hva er cos(330°) ?,
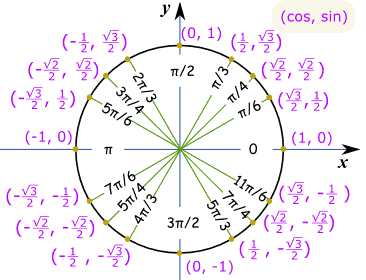
Lag en skisse som dette, og vi kan se at det er den «lange» verdi: √32 Og dette er det samme Apparatet Sirkel i radianer.
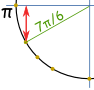
Eksempel: Hva er synd(7π/6) ?
Tror «7π/6 = π + π/6», og deretter lage en skisse. Vi kan se det som er negativt og er «liten» verdi: −½ |