Innhold – Konstant akselerasjon

Innhold

Konstant akselerasjon

Vi er alle kjent med det faktum at en bil hastigheter opp når vi setter vår fot ned på gasspedalen. Frekvensen av endring av hastigheten til en partikkel med hensyn til tid er kalt sin akselerasjon. Hvis hastigheten til partikkelen endringer på en konstant hastighet, så denne prisen kalles konstant akselerasjon.,

For eksempel, hvis hastigheten til en partikkel som beveger seg i en rett linje endringer jevnt (på en konstant hastighet på endre) fra 2 m/s 5 m/s over ett sekund, da er det konstant akselerasjon er 3 m/s\(^2\).

Avtagende hastighet

Hvis en partikkel har en innledende hastighet på 6 m/s og en konstant akselerasjon av \(-2\) m/s\(^2\), trykk deretter:

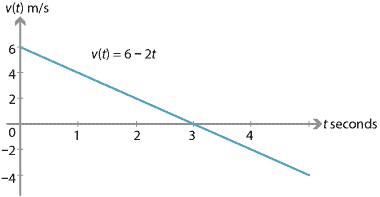
i Løpet av de første tre sekunder, partikkel er hastigheten er avtagende (partikkel er bremse ned). På tre sekunder, partikkel er et øyeblikk i ro., Etter tre sekunder, hastigheten er fortsatt synkende, men hastigheten er økende (partikkelen går raskere og raskere).

Oppsummering

Hvis vi antar at endring av hastighet (akselerasjon) er en konstant, deretter konstant akselerasjon er gitt ved

\

Mer presist, den konstant akselerasjon \(a\) er gitt ved formelen

\

hvor \(v(t_i)\) er hastigheten på tidspunktet \(t_i\). Siden hastighet er en vektor, så er akselerasjon.,

Den konstant akselerasjon formler for bevegelse i en rett linje

i denne delen, vi har vært vurderer bevegelse i en rett linje med konstant akselerasjon. Denne situasjonen er svært vanlig, for eksempel, en kropp i bevegelse under påvirkning av tyngdekraften reiser med en konstant akselerasjon.

Det er antatt at bevegelse begynner når \(t = 0\), og at den første posisjonen er tatt som opprinnelse, som er \(x(0) = 0\).,

De fem ligninger av bevegelse

1. \(v = u + til\)
2. \(x = \dfrac{(u+v)t}{2}\)
3. \(x = ut + \dfrac{1}{2}p^2\)
4. \(v^2 = r^2 + 2ax\)
5. \(x = vt – \dfrac{1}{2}p^2\)

Merk. Hver av de fem ligninger involverer fire av de fem variablene \(u, v, x, a, t\). Hvis verdiene av tre av variablene er kjent, vil de gjenværende verdiene kan bli funnet ved å bruke to av ligningene.,

Kommer det konstant akselerasjon formler

Den første ligningen av bevegelse

Siden akselerasjonen er konstant, har vi \(a = \dfrac{v-u}{t}\). Dette gir den første ligningen av bevegelse, \(v = u + til\).

Den andre ligningen av bevegelse

Den andre ligningen,

\

sier at vekt er oppnådd ved å multiplisere gjennomsnittet av første og siste fart av den tiden som har gått under bevegelse. Mer rett og slett:

\

Vi kan utlede denne ligningen ved hjelp av det faktum at vekt er lik det registrerte arealet under fart–tid-grafen.,

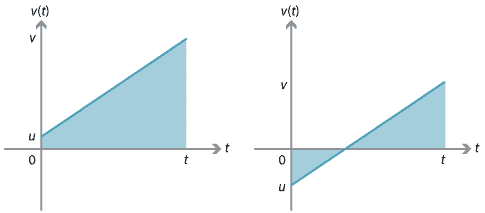
For grafen til høyre, vekt kan bli funnet ved å vurdere de to trekantene mellom grafen og \(t\)-aksen. En av trekantene har positiv signert området og den andre har negative signert området.

Finne vekten av en partikkel fra velocity–tid grafen ved hjelp av integrering vil bli diskutert i en senere del av denne modulen.,

Den tredje ligningen av bevegelse

Erstatter \(v\) fra den første ligningen inn i den andre likningen gir

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+i)t}{2} \\ &= \dfrac{2ut+i^2}{2} \\ &= ut + \dfrac{1}{2}p^2, \end{align*}

som er den tredje ligningen. Dermed \(x\) er en kvadratisk i \(t\), og dermed grafen til \(x\) mot \(t\) er en parabel.

Den fjerde bevegelseslikning

Fra den første ligningen, vi har \(t = \dfrac{v-u}{a}\)., Å erstatte dette inn i den andre likningen gir

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2} \\ &= \dfrac{v^2-u^2}{2}. \end{align*}

Omorganisere å gjøre \(v^2\) emnet gir den fjerde ligningen: \(v^2 = r^2 + 2ax\).

Den femte bevegelseslikning

Fra den første ligningen, vi har \(u = v-i\)., Ved hjelp av den andre ligningen, får vi

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-i+v)t}{2} \\ &= \dfrac{2vt-på^2}{2} \\ &= vt-\dfrac{1}{2}p^2, \end{align*}

som den femte ligningen.

Vertikal bevegelse

Bevegelse på grunn av tyngdekraften er en god kontekst for å demonstrere bruken av konstant akselerasjon formler., Som diskutert tidligere, våre to retningene i vertikal bevegelse opp og ned, og en avgjørelse må gjøres med hensyn til hvilken av de to retningene er positive. Akselerasjon på grunn av tyngdekraften er en konstant, med magnitude merket med \(g\). I følgende eksempel vil vi ta oppover retning for å være positiv og ta \(g = 10\) m/s\(^2\).

Videre bruk av ligningene for bevegelse

Next page – Content – Average velocity and average speed