Søk Alle Røttene til et Polynom Funksjon
Bruk vpasolve for å finne alle løsningene til funksjonen f(x)=6×7-2×6+3×3-8.
– >
syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)
vpasolve returnerer syv røtter av funksjonen, som forventet, fordi funksjonen er et polynom av grad sju.,
Søk Nuller i en Nonpolynomial Funksjon ved Hjelp av Søk-Områder og Utgangspunkt
Et plott av funksjonen f(x)=e(x/7)cos(2x) avslører periodisk nuller, med økende bakkene på null poeng som x øker.
– >
syms xh = fplot(exp(x/7)*cos(2*x),);grid on
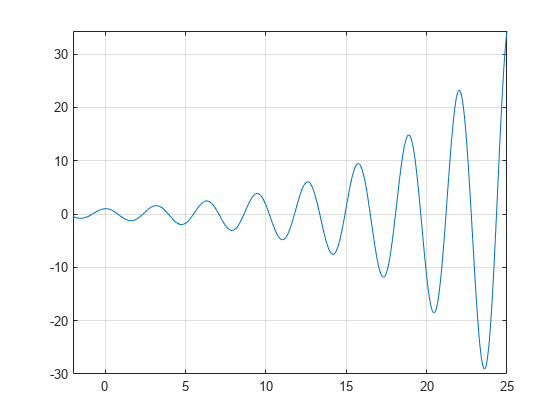
Bruk vpasolve for å finne et nullpunkt for funksjonen f. Merk at vpasolve returnerer bare en løsning av en nonpolynomial ligning, selv om flere løsninger finnes., On repeated calls, vpasolve returns the same result.
f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.
for k = 1:3 vpasolve(f,x,'Random',true)end
ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')
ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')
ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')
To find a zero close to x=10, set the starting point to 10.,
– >
vpasolve(f,x,10)
– >
ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')
for Å finne nær null for x=1000, angi startpunktet til 1000.
– >
vpasolve(f,x,1000)
– >
ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')
for Å finne null i området 15≤x≤25, angi søk utvalg til .,
– >
vpasolve(f,x,)
– >
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
for Å finne flere nuller i området , du kan ikke ringe vpasolve gjentatte ganger, fordi det gir det samme resultatet på hver samtale, som tidligere vist. I stedet, satt søk utvalg og angi 'Random' til true.,
– >
for k = 1:3 vpasolve(f,x,,'Random',true)end
– >
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
– >
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
– >
ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')
Fordi 'Random' velger utgangspunkt tilfeldig, den samme løsningen kan bli funnet på påfølgende anrop.,
Finn Alle Nuller er det i en Spesifisert Søk Spekter
Lag en funksjon findzeros for å systematisk finne alle nuller for f i et gitt søk utvalg, innen en angitt feil toleranse. Funksjonen starter med innspill søk utvalg og samtaler vpasolve for å finne en null. Så, det splitter søk-området i to rundt null verdi og undermapper kaller seg selv med nye søk områder som input for å finne flere nuller.
funksjonen er forklart delen av avsnittet her.,
Erklære funksjon med tre innganger og én utgang. Den første innspill er funksjonen, den andre inngangen er omfanget, og eventuelt tredje inngang lar deg angi feil mellom null og høyere og lavere grenser som er generert fra det.
function sol = findzeros(f,range,err)
Hvis du ikke angi valgfritt argument for feil toleranse, findzeros angir err til 0.001.
if nargin < 2 err = 1e-3;end
Finn en null i søk-område ved hjelp av vpasolve.,
sol = vpasolve(f,range);
Hvis vpasolve finner ikke et null, du avslutt.
if(isempty(sol)) return
Hvis vpasolve finner et nullpunkt, split søk-området i to søk områder over og under null.
else lowLimit = sol-err; highLimit = sol+err;
Ring findzeros med lavere søk utvalg. Hvis findzeros returnerer nuller, kopiere verdiene i løsningen utvalg og sortere dem.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end
Ring findzeros med høyere søk utvalg., Hvis findzeros returnerer nuller, kopiere verdiene i løsningen utvalg og sortere dem.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend
hele funksjon findzeros er som følger. Lagre denne funksjonen som findzeros.m i den gjeldende mappen.
– >
syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'
Få Løsninger for Vilkårlig Presisjon
Bruk digits for å angi presisjon av løsninger som returneres av vpasolve., Som standard vpasolve returnerer løsninger til en presisjon på 32 viktige tall.
– >
f = exp(x/7)*cos(2*x);vpasolve(f)
– >
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
Bruk digits for å øke presisjonen til 64 viktige tall. Når du endrer digits kontroller at du lagrer den gjeldende verdien, slik at du kan gjenopprette det.,
– >
digitsOld = digits;digits(64)vpasolve(f)
– >
ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')
Neste, endre presisjon av løsninger til 16 viktige tall.
– >
digits(16)
Løse Multivariate Ligninger ved Hjelp av Søk Varierer
bør du Vurdere følgende system av ligninger.
z=10(cos(x)+cos(y))z=x+y2-0.1x2yx+y-2.7=0
En tomt av ligninger for 0≤x≤2,5 og 0≤x≤2.5 viser at de tre flater som skjærer hverandre i to punkter., For å bedre synliggjøre tomten, bruk view. Å skalere fargekartet verdier, kan du bruke caxis.
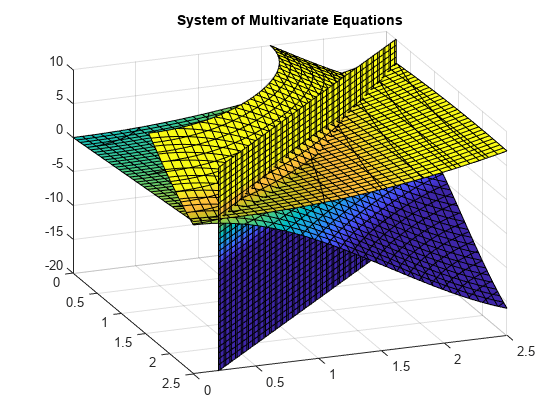
Bruk vpasolve for å finne et punkt hvor den flater møtes. Funksjonen vpasolve returnerer en struktur. For å få tilgang til x-, y – og z-verdier av løsningen, indeks i strukturen.,
– >
sol = vpasolve(equations);
for Å søke i et område av løsningen plass, angi søk områder for variablene. Hvis du angir områder 0≤x≤1.5 og 1.5≤y≤2.5, så vpasolve funksjonen søker avgrenset område vises.

Bruk vpasolve for å finne en løsning for dette søket utvalg. Hvis du vil utelate et søk utvalg for z, angi tredje søk utvalg til .,
– >
vars = ;range = ;sol = vpasolve(equations, vars, range);
for Å finne flere løsninger, setter 'Random' alternativ til true. Dette gjør vpasolve bruk tilfeldig startpunkt på etterfølgende kjøringer. 'Random' alternativet kan brukes i forbindelse med søk områder for å gjøre vpasolve bruk tilfeldig utgangspunkt i et søk utvalg. Fordi 'Random' velger utgangspunkt tilfeldig, den samme løsningen kan bli funnet på påfølgende anrop., Ring vpasolve gjentatte ganger for å sikre at du finner begge løsninger.
Plotte differensialligninger. Overlappe løsninger som et punktplott av punkter med gul X markører ved hjelp av scatter3. For å bedre synliggjøre tomten, må to av de gjennomsiktige overflater ved hjelp av alpha. Skala fargekartet til tomten verdier ved hjelp av caxis, og endre perspektivet ved hjelp av view.
vpasolve finner løsninger i skjæringspunktet mellom flater som er dannet av ligninger som vist.,

Lastly, restore the old value of digits for further calculations.
digits(digitsOld)