På disse sidene ser vi på noen interessante konsepter, ser vi på buede plass: hva buet plass betyr, hvordan vi kan fortelle om en plass som er buet fra innsiden eller utenfor den.
Vi se på hvordan vi kan bygge inn på typen plass inne i en annen og se at vi kan kartet, mellom ulike områder og på ulike måter.
Vi også se på compacification og hvordan vi kan representere uendelig stort og infinitesimally små vektorer i våre områder er på måter som ikke fører ikke til singularities og andre problemer.,
Disse begrepene vise seg å være nyttig, selv når vi arbeider med flatskjerm plass, vil vi finne måter å representere vektorer og fly som ikke går gjennom origo. Dette gir oss måter å representere rotasjoner og oversettelser som en enkelt operasjon.
Det andre programmet er relativistiske rom-tid.
Rienmannian Geometri
I Rienmannian geometri plass kan skru på forskjellige steder (se mangfoldigheter) her ser vi på geometrier hvor kurven på plass er konstant.,
Eulidean Geometri
flatskjerm plass,
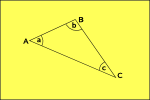
Hyperbolsk Geometri
plass kurver ytre
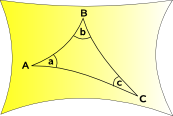
Sfærisk Geometri og Elliptiske Geometri
plass kurver innover
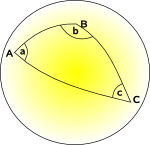
I en buet (Non-Euclidean) geometri vi ikke kan finne et sett av koordinater som er vinkelrette, der koordinere linjer er alle parallelle til hverandre, og hvor hver grid square har samme område., Vi kan muligens finne et koordinatsystem der vi kan gjøre noen av disse, men ikke alle.
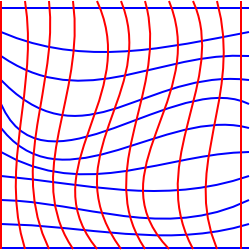
Dette diagrammet prøver å illustrere denne situasjonen i 2 dimensjoner, selv om det er litt misvisende, fordi vi har trukket det på et fly slik at vi kunne ha trukket rektangulære koordinater.
for Å prøve å illustrere en situasjon hvor dette er umulig kunne vi tenke på en to-dimensjonale fly som har blitt strukket inn i den tredje dimensjonen.,

I denne situasjonen kan vi velge koordinater som danner et rektangulært rutenett når projisert på et horisontalt plan, men til en person som lever i overflaten, må noen av nettet rutene vil synes å ha et større område enn andre, og linjene i rutenettet kan ikke ser ut til å være parallelle. Det er ingen to-dimensjonalt koordinatsystem som vil bevare parallelle linjer, vinkler og arealer på samme tid.,
Et lignende eksempel er å prøve å kartlegge overflaten av jorden, kan vi bruke breddegrad og lengdegrad linjer, men lengdegrad linjer komme nærmere nærmere polene.
I disse tilfeller vil vi kunne arbeide i form av 3-dimensjonale koordinater, og det er en tilnærming som vi vil ta med noen typer av non-Euclidean geometrier. Det er ofte mulig å legge inn en bestemt geometri i en høyere dimensjonal geometri for å gjøre det mer Euclidean.,
noen ganger er Det slik at når vi ser på en geometri på en stor skala at det er non-Euclidean, men hvis vi ser på det på en mindre og mindre skala, så det er tilnærmet lik en Euclidean geometry. For å gjøre dette trenger vi for å finne et koordinatsystem der vinkler er bevart på alle punkt, som er, horisontal og vertikal koordinering linjer må alltid møtes i 90°, selv om linjene ikke kan være rett. Dette er kjent som en konforme geometri. I denne type geometri vi kan i det minste definere et lokalt koordinatsystem.,
Knyttet til dette, er om geometri kan være differensiert og integrert, en forutsetning for dette er at det må være oppførte seg bra og ikke har noen plutselige hopp etc. Noen geometrier og samordne systemer kan være oppførte seg bra i noen steder, men har singularities etc.
For diskusjon om hvordan kurvatur er målt se denne siden.
Matematisk Notasjon
Hvordan kan vi håndtere geometrier, der vi ikke kan bruke alle de regler som gjelder for euclidean geometry?,
En tilnærming er å bruke tensoren notasjon, dette gir konvensjoner og notasjon som kan hjelpe oss i å bytte mellom forskjellige koordinatsystem. Et rettvinklet koordinatsystem, lokale til et punkt, kan defineres ved hjelp av grunnlag vektorer som er tangenter til å koordinere linjer.,Manifold
du vil se denne siden
Forholdet mellom Hyperbolske og Minkowski Geometrier
| Minkowski Geometri | Hyperbolsk Geometri | |
| punkt | event i verdensrommet tid | partikkel i en ensartet bevegelse |
| avstanden mellom to punkt | plass-tidsintervallet mellom to hendelser | relative hastigheten mellom to slike partikler |
Terminologi
Her ser vi på den terminologi som geometrier, mellomrom, modeller, prognoser og forvandler., Det er ganske vanskelig når vi begynner å gjøre med non-Euclidean geometrier, fordi vi bruker lignende terminologi som vi er vant til i vanlig Euclidean plass, men vilkårene kan ha litt forskjellige egenskaper.,prøv
Elliptic Geometri
– Modeller
Eksempler er:
- Øvre halvdel-flyet modell
- Poincare disc modellen
- Projektiv modell
- Konforme modell
Anslag
Stereografisk Projeksjon
Forvandler
Invariant
Eksempler er:
- Möbius Forvandle
- Lorentz Forvandle
Parallell Postulat
Hvis vi tar bort de parallelle postulat fra Euclidean Plass.,
Dette fører til:
- parallell postulat er false
- vinklene i en trekant ikke legge til π
- for en form av en gitt størrelse, er det ikke generelt, finnes en tilsvarende form av en større størrelse.,ctive
– konforme (Poincaré-plate ) rette linjer – geodesics segmenter av sirkler vinkel bevare mer indre vinklene i trekanten π-(α+β+γ)=CΔ avstanden mellom to punkt med