En null-hypotesen er en presis redegjørelse om en befolkning som vi prøver å avvise med eksempel data.Vi vanligvis ikke har tro på at vår nullhypotesen (eller H0) til å være sant. Men vi trenger noen eksakte setningen som et utgangspunkt for statistisk signifikanstesting.
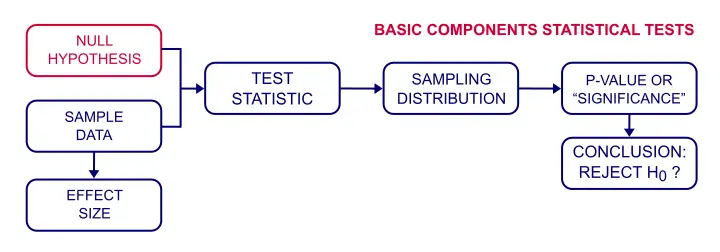
nullhypotesen Eksempler
Ofte-men ikke alltid – nullhypotesen sier det er ingen forening eller forskjellen mellom variabler eller undergrupper., Som så, noen typiske null-hypoteser er:
- korrelasjonen mellom frustrasjon og aggresjon er null (korrelasjon-analyse);
- gjennomsnittlig inntekt for menn er lik som for kvinner (independent samples t-test);
- Nasjonalitet (perfekt) som ikke er relatert til musikk preferanse (chi-square uavhengighet test);
- den gjennomsnittlige befolkningen inntekt var lik over 2012 til og med 2016 (gjentatt tiltak ANOVA).
«Null» Ikke Betyr «Null»
En vanlig misforståelse er at «null» impliserer «null». Dette er ofte, men ikke alltid tilfelle., For eksempel, en null-hypotesen kan også state thatthe korrelasjon mellom frustrasjon og aggresion er 0.5.Ingen null involvert her, og -selv om noe uvanlig – helt gyldig.
«null» i «nullhypotesen» stammer fra «opphever»5: nullhypotesen er uttalelsen som vi prøver å tilbakevise, uansett om den gjør det (ikke) angir en null effekt.
Null-Hypotese-Testing -Hvordan Fungerer Det?
jeg ønsker å vite om lykke er knyttet til rikdom blant nederlandske folk. En tilnærming til å finne dette ut på er å formulere en null-hypotese., Siden «i forhold til» er ikke presis, vi velger det motsatte uttalelse som vår nullhypotesen:det korrelasjon mellom rikdom og lykke er null blant alle nederlandske folk.Vi vil nå prøve å avkrefte denne hypotesen for å vise at lykke og rikdom er i slekt all right.
Nå, vi kan ikke med rimelighet stille alle 17,142,066 nederlandske folk hvor glade de generelt føler deg.

Slik at vi vil stille et eksempel (si, 100 folk) om sin rikdom og sin lykke. Sammenhengen mellom lykke og velstand viser seg å være 0,25 i vårt eksempel., Nå har vi ett problem: eksempel på resultater har en tendens til å avvike noe fra befolkningen utfall. Så hvis korrelasjonen er virkelig null i vår populasjon, kan vi finne en ikke null korrelasjon i vårt eksempel. For å illustrere dette viktige punktet, ta en titt på scatterplot nedenfor. Det synliggjør en null korrelasjon mellom lykke og rikdom for en hel populasjon på N = 200.

Nå er vi trekke et tilfeldig utvalg av N = 20 fra denne populasjonen (de røde prikkene i vår forrige scatterplot). Selv om befolkningen vår sammenheng er null, har vi funnet en svimlende 0.,82 korrelasjon i vårt eksempel. Figuren nedenfor illustrerer dette ved å utelate alle ikke samplet enheter fra våre tidligere scatterplot.

Dette reiser spørsmålet hvordan vi kan noensinne si noe om befolkningen vår hvis vi bare har en liten prøve fra det. Den grunnleggende svar: vi kan sjelden si noe med 100% sikkerhet. Men, vi kan si mye med 99%, 95% eller 90% sikkerhet.
Sannsynligheten
Så hvordan gjør man det? Vel, i utgangspunktet, noen eksempler på resultatene er svært lite sannsynlig gitt våre nullhypotesen., Som så, figuren nedenfor viser sannsynligheter for eksempel ulike sammenhenger (N = 100) hvis befolkningen korrelasjon virkelig er null.

En datamaskin kan lett beregne disse sannsynlighetene. Imidlertid, å gjøre det krever et eksempel størrelse (100 i vårt tilfelle) og en antatt befolkning korrelasjon ρ (0, i vårt tilfelle). Så det er derfor vi trenger en null-hypotese.
Hvis vi ser på dette prøvetaking distribusjon nøye, ser vi at prøven sammenhenger rundt 0 er mest sannsynlig: det er en 0.68 sannsynligheten for å finne en sammenheng mellom -0.1 og 0.1. Hva betyr det?, Vel, husk at sannsynlighetene kan bli sett på som relative frekvenser. Så tenk vi vil trekke i 1 000 prøver i stedet for den vi har. Dette vil resultere i 1,000 korrelasjon koeffisienter og noen 680 av dem -en relativ frekvens av 0.68 – ville være i området -0.1 til 0.1. På samme måte, det er en 0.95 (eller 95%) sannsynligheten for å finne et eksempel på sammenheng mellom -0.2 og 0,2.
P-Verdier
Vi funnet et eksempel korrelasjon på 0,25. Hvor sannsynlig er det at hvis befolkningen korrelasjon er null?, Svaret er kjent som p-verdi (kort for sannsynligheten verdi):En p-verdien er sannsynligheten for å finne noen eksempler på resultat eller en mer ekstrem hvis nullhypotesen er sann.Gitt våre 0.25 korrelasjon, «mer ekstrem» betyr vanligvis større enn 0,25 eller mindre enn -0.25. Vi kan ikke fortelle fra vår grafen, men den underliggende tabellen forteller oss at p ≈ 0.012. Hvis nullhypotesen er sann, det er en 1,2% sannsynlighet for å finne vårt eksempel korrelasjon.
Konklusjonen?
Hvis befolkningen vår sammenheng egentlig er null, så vi kan finne et eksempel korrelasjon på 0,25 i en prøve med N = 100., Sannsynligheten for at dette skjer er bare 0.012, så det er svært lite sannsynlig. En rimelig konklusjon er at befolkningen vår sammenheng var ikke null etter alle.
Konklusjon: vi forkaster nullhypotesen. Gitt vårt eksempel utfallet, er vi ikke lenger tror at lykke og rikdom er urelaterte. Men vi kan fortsatt ikke fast dette med sikkerhet.
nullhypotesen – Begrensninger
så langt, vi har bare konkluderte med at befolkningen sammenheng er trolig ikke er null. Det er den eneste konklusjonen fra vår nullhypotesen tilnærming, og det er egentlig ikke så interessant.,
Hva vi virkelig ønsker å vite, er befolkningen korrelasjon. Vår eksempel korrelasjon på 0,25 virker som et rimelig anslag. Vi kaller et slikt enkelt nummer en punktestimatet.
Nå, en ny prøve kan komme opp med en annen sammenheng. Et interessant spørsmål er hvor mye vårt eksempel sammenhenger ville svinge over prøver hvis vi vil trekke mange av dem. Figuren nedenfor viser nettopp at, antar utvalget vårt størrelse med N = 100 og vår (punkt) estimat på 0,25 for befolkningen korrelasjon.,

konfidensintervaller
eksempel resultatet tyder på at omtrent 95% av mange prøver bør komme opp med en korrelasjon mellom 0.06 og 0.43. Dette området er kjent som et konfidensintervall. Selv om det ikke nettopp er riktig, er det mest lett selv på som den båndbredden som er sannsynlig å vedlegge befolkningen korrelasjon.
En ting å merke seg er at concidence intervall er ganske bredt. Det er nesten inneholder en null korrelasjon, akkurat nullhypotesen vi avviste tidligere.,
en Annen ting å merke seg er at våre prøvetaking distribusjon og konfidensintervall er litt asymmetrisk. De er symmetriske for de fleste andre statistikk (som betyr eller beta-koeffisienter), men ikke korrelasjoner.