
har du noen gang lurt på hvordan kan det snø på over minusgrader? Vel, naiv forklaring er at det tar rett og slett tid for snøkrystallene til å smelte når de trenge over frysepunktet luften, som de stige ned til bakken. Dette, selvfølgelig, er grunnen til at hagl kan falle i varmt vær. Ganske enkelt, hagl faller fort, altfor fort for å la den varme luften smelte hagl. Dette er ikke den viktigste forklaringen, men for hvorfor det kan snø når det er over frysepunktet.,
Fra figuren nedenfor, det er tydelig at det er en klar avhengighet på fuktighet – tørrere det er, jo varmere kan det være mens snø. Dette innebærer at den viktigste faktoren, i det minste i tørre omgivelser, og har å gjøre med fuktighet. Og denne faktoren er fordamping. Mer spesifikt, som snøflak ned, fordampe. Denne prosessen tar varme og holder flak kaldt.
Derfor, hvis vi ønsker å beregne den maksimale temperaturen, vi trenger for å beregne netto strålingsbalanse av flasse. For det første, som flak reise i et varmt miljø, kan de få varme fra det omkringliggende gjennom ledning., For det andre, varmen brukes til å fordampe flak, og dermed kjøling dem. Hvis fordamping varme «vask» er større enn varmeledning, flak vil forbli frosset.
Det viser seg at dette kan være lett beregnes. Nei, det er ikke enkelt å beregne varmeledning eller fordampning varme, men forholdet er, siden ulike ukjent geometriske faktorer kansellere ut.
Hvis du ikke bryr deg om beregning (fordi du ikke er en vitenskap freak), kan du bare gå til kalkulator side.
Hvis du ikke bryr deg, her er det avledning., La oss anta at flyte rundt flak er slik at en grense lag med bredde d former rundt det. Den totale varmestrømmen $F_H$ til flake (f.eks., J/sek i MKS) vil være gitt ved Fourier ‘ s lov:
hvor $\kappa$ er varme spredning koeffisient av luft (f.eks., m2/sek i MKS), c er varmekapasitet for luft (J/kg i MKS), A er arealet av grenselaget rundt flake, mens ΔT er temperaturforskjellen mellom skalle og miljø.,
på samme måte kan man bruke Fick ‘ s lov å få diffusjon av vanndamp fra flake (der temperaturen er nær frysepunktet, og den relative luftfuktigheten er 100%), til det omkringliggende miljø, der temperaturen er høyere og den relative luftfuktigheten lavere:
Her, D er vann diffusjon koeffisient (f.eks., m2/sek i MKS) og ρ er vanndamp tetthet (kg/m3 i MKS).,
fordamper is krever varme, dermed, hvis det er en vanndamp masse flux av Φ fra flake, det ville kreve varme til en pris av $F_w = \epsilon \Phi$ hvor $\epsilon$ er varmen av dampfunksjon av is (J/kg i MKS).
Det høyeste temperatur over som snøfnugg som smelter, er temperaturen som de to varme strømmer er lik:
vær Oppmerksom på at geometri og flyte rundt flake går ut, fordi den både varme fluksene avhenger d og En på samme måte., Dette vil være tilfelle også hvis grenselaget rundt flake er komplekse, slik at d faktisk er avhengig av retningen. Derfor,
hvor $\rho_{satt}$ er metning vanndamp tetthet.
Koble til tallene (som kan finnes for eksempel i CRC handbook of kjemi og fysikk), resultater, med en implisitt ligning for temperaturebecause metning vanndamp tetthet avhenger av temperaturen, så vel., Vi kan forenkle ting hvis vi i stedet spørre hva som er den relative fuktighet som kreves for å holde flake frosset ved en gitt temperatur. Det er:
hvor $T_C$ er temperaturen i grader Celsius.
Denne funksjonen kan sees i figuren under, sammen med data fra Matsuo og Sasyo, 1981. Som en kan se fra figur, er det beregnet grafen er omtrent den nedre grensen nedenfor der det ikke regn i det hele tatt. Ved varmere temperaturer, det er en blanding., Opp til ca 1°C over ikke å smelte linje, det er mest snø mens mellom 1°C og 2°C over streken, det er for det meste regn, men snø er mulig. Disse hendelsene kan være grunn til ekstra effekter, slik som sterke downdrafts, tiden det tar å smelte snøen, etc.
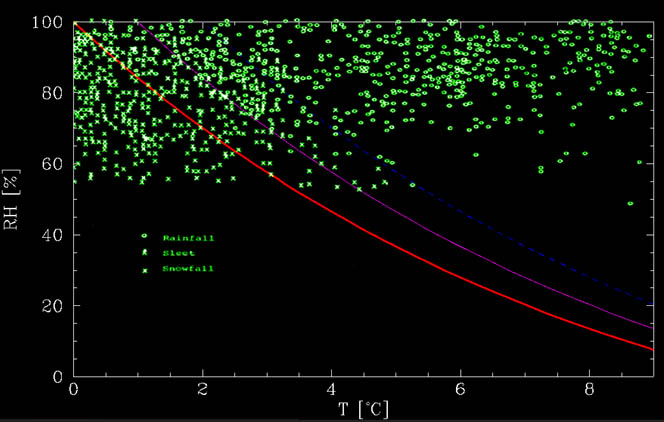
Dermed, hvis vi ønsker å observere været er varmt, snø, svært tørre forhold er nødvendig. For eksempel, hvis bakken fuktighet er bare ca 20% (svært sjelden, fordi hvis det er nedbør, atmosfæren er generelt våt!) så kan det snø på 8°C (eller 46°F for engelsk brukere).,
et Annet krav er at ingen steder langs stige gjør luften overgå ingen smelte linje. Hvis den gjør det, flake vil selvfølgelig smelte.
Hvis temperaturen ikke stiger over frysepunktet, det er det ingen parametre med hvilken type nedbør kan fastslås med sikkerhet. Alle som så kan vi forutsi er sannsynligheten for at snø vil faktisk faller. Dette kan gjøres ved hjelp av resultatene av Häggmark og Ivarsson (1997), bare ved å bruke frossen-pære og ikke wet-bulb temperatur.
Den nederste linjen er en kalkulator som sannsynligheten for at snø kan estimeres.,