tverrsnitt

Egenskaper av Områder

Centroid

centroid i en form som representerer punktet om hvilket område av den delen er jevnt fordelt. Hvis området er dobbelt symmetrisk om to ortogonale akser, den centroid ligger i skjæringspunktet mellom disse aksene. Hvis området er symmetrisk om bare én akse, så centroid ligger et eller annet sted langs den aksen (den andre koordinere må beregnes)., Hvis den nøyaktige plasseringen av centroid kan ikke påvises ved inspeksjonen, det kan beregnes ved:

hvor dA representerer området en infinitesimally liten del, er det totale arealet av tverrsnittet, og x og y koordinatene til rette element dA med hensyn til den aktuelle aksen.,

centroidal steder av vanlige tverrsnitt er godt dokumentert, så det er vanligvis ikke nødvendig å beregne plasseringen din med ligningene ovenfor., av grunnleggende former som centroidal steder som er kjent med hensyn til noen referanse punkt, så centroidal beliggenhet i det sammensatte tverrsnitt kan beregnes som:

hvor xc,jeg og yc,jeg er den rektangulære koordinater centroidal plasseringen av ed delen med hensyn til referansepunkt, og Ai er det området av ed-delen.,

Centroidal Avstand

centroidal avstand, c, er avstanden fra centroid av et tverrsnitt av den ekstreme fiber., Den centroidal avstand i y-retning for et rektangulært tverrsnitt er vist i figuren nedenfor:

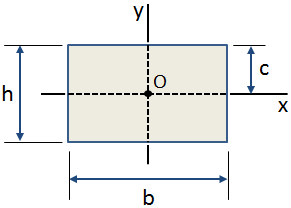
Vanlige bruksområder for centroidal avstand inkluderer:

• for å beregne den maksimale bøyestyrke i et tverrsnitt
• beregning av verdien av det første øyeblikk av området, Q, over et punkt i tverrsnittet til å bestemme skjærspenning ved at punkt

Første Øyeblikk av Området

første øyeblikk av et område med hensyn til en akse av interesse er beregnet som:

Qx = ∫ y dA

Qy = ∫ x dA

hvor Qx er den første moment om x-aksen og Qy er den første moment om y-aksen.,Hvis området er sammensatt av en samling av grunnleggende former som centroidal steder som er kjent med hensyn til aksen som er av interesse, da det første øyeblikk av kompositt-området kan beregnes som:

Merk at det første øyeblikk av området er brukt ved beregning av centroid av et tverrsnitt med hensyn til noen opprinnelse (som nevnt tidligere)., Det første øyeblikket er også benyttet ved beregning av verdien av skjærspenning ved et bestemt punkt i tverrsnittet. I dette tilfellet, vil den første øyeblikket er beregnet for et område som utgjør en mindre del av tverrsnitt, hvor området er avgrenset av punkt av interesse og ekstreme fiber (toppen eller bunnen) av tverrsnitt. Det første øyeblikket er beregnet om en akse som går gjennom centroid av tverrsnitt.,

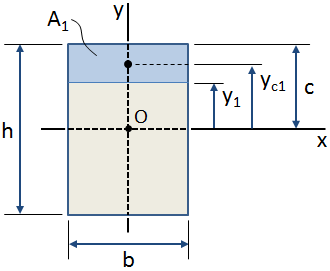
I figuren ovenfor, skravert blått område er område av interesse innen hele tverrsnitt.,nt på dette området med hensyn til x-aksen (som passerer gjennom tverrsnitt centroid, punkt O i figuren over) er beregnet som:

Hvis centroidal beliggenhet i området av interesse er kjent, da det første øyeblikk av området med hensyn til aksen kan beregnes som (se figuren over):

Det bør bemerkes at den første øyeblikket av et område vil være positiv eller negativ, avhengig av posisjonen til den posisjonen i området med hensyn til den aktuelle aksen., Derfor, den første øyeblikket av hele området av et tverrsnitt med hensyn til sin egen centroid vil være null.

– Området treghetsmoment

Den andre øyeblikk av området, mer kjent som treghetsmoment, jeg, av et tverrsnitt er en indikasjon på en strukturell medlemmets evne til å motstå bøye.,(Note 1) Ix og Iy er de øyeblikk av treghet om x – og y – aksene, henholdsvis, og beregnes ved:

Ix = ∫ y2 dA

Iy = ∫ x2 dA

der x og y er koordinatene til rette element dA med hensyn til den aktuelle aksen.

vanligvis, de øyeblikkene av treghet er beregnet med hensyn til den delen er centroid. I dette tilfellet er de referert til som centroidal øyeblikk av treghet og er betegnet som Icx for treghet om x-aksen og Isete for treghet om y-aksen.,

øyeblikk av treghet i vanlige tverrsnitt er godt dokumentert, så det er vanligvis ikke nødvendig å beregne dem med ligningene ovenfor. Egenskaper av flere vanlige tverrsnitt er gitt på slutten av denne siden.

Hvis et tverrsnitt er sammensatt av en samling av grunnleggende former som centroids er alle sammenfallende, så treghetsmoment av kompositt-delen er bare summen av de enkelte øyeblikk av treghet. Et eksempel på dette er en boks stråle som består av to rektangulære deler, som vist nedenfor., I dette tilfellet, den ytre delen har «positiv område» og den indre delen har «negativ området,» så kompositt treghetsmoment er subtraksjon av treghetsmoment av den indre delen av ytre delen.

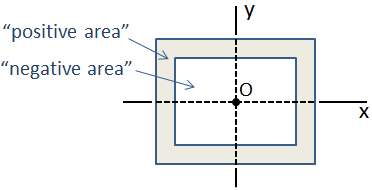
I tilfelle av en mer komplisert sammensatt tverrsnitt som centroidal steder er ikke sammenfallende, treghetsmoment kan beregnes ved hjelp av parallell akse teorem.

Det er viktig ikke å forveksle treghetsmoment av et område med masse treghetsmoment av en solid kropp., Området treghetsmoment viser et tverrsnitt er motstand mot bøying, mens massen treghetsmoment indikerer en kroppens motstand mot rotasjon.,

Parallell Akse Teorem

Hvis treghetsmoment av et tverrsnitt om en centroidal aksen er kjent, og parallelt med aksen teorem kan brukes til å beregne treghetsmoment om noen parallell akse:

hvor Ic er treghetsmoment om centroidal aksen, d er avstanden mellom centroidal aksen og parallelt med aksen, og A er arealet av tverrsnittet.,

Hvis et tverrsnitt er sammensatt av en samling av grunnleggende former som centroidal øyeblikk av treghet er kjent sammen med avstander på centroids til noen referanse punkt, og deretter parallell akse teorem kan brukes til å beregne treghetsmoment i det sammensatte tverrsnitt.

For eksempel, en tekstmarkør kan du oppnå ved 3 rektangler, som vist nedenfor. Siden dette kompositt delen er symmetrisk om både x – og y – aksene, den centroid av seksjon kan være plassert ved inspeksjon i skjæringspunktet mellom disse aksene. Den centroid er plassert i origo, O, i figuren.,

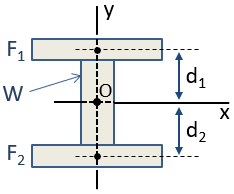
treghetsmoment av kompositt-delen kan beregnes ved hjelp av parallell akse teorem. Den delen er centroidal treghetsmoment om x-aksen, Icx, er beregnet som:

hvor Icx vilkårene er de øyeblikk av treghet i de enkelte avsnittene om sin egen centroids i retning av x-aksen, d vilkårene er avstandene av den individuelle delen centroids til kompositt delen centroid, og En vilkårene er de områdene av de enkelte deler. Fordi centroid delen av W og centroid av kompositt-delen er sammenfallende, d er null for at delen og så det er ingen Ad2 sikt.,

Det er viktig å merke følgene av parallell akse teorem som en enkelt punkt beveger seg lengre fra centroid av kompositt-delen, bidrag av denne delen til den sammensatte delen er treghetsmoment øker med en faktor på d2. Derfor, hvis hensikt er å øke treghetsmoment av et avsnitt om en bestemt akse, det er mest effektivt å finne område så langt fra at aksen som mulig. Dette forklarer form av en tekstmarkør., Flensene er den primære bidragsytere til treghetsmoment, og web-tjener til å skille flenser fra bøying aksen. Nettet trenger å beholde en viss tykkelse imidlertid å unngå knekking og fordi nettet tar en betydelig del av skjærspenning i avsnittet.

Polare treghetsmoment

Det polare treghetsmoment, jeg, av et tverrsnitt er en indikasjon på en strukturell medlemmets evne til å motstå torsjon om en akse vinkelrett på den delen., Det polare treghetsmoment for en del med hensyn til en akse kan beregnes ved:

der x og y er koordinatene til rette element dA med hensyn til den aktuelle aksen, og r er avstanden mellom element dA den aktuelle aksen.,

Selv om det polare treghetsmoment kan beregnes ved hjelp av formelen ovenfor, det er vanligvis mer praktisk å beregne det å bruke loddrett akse teorem, som sier at det polare treghetsmoment av et område som er summen av de øyeblikkene av treghet om to ortogonale akser som passerer gjennom aksen av interesse:

vanligvis, den aktuelle aksen går gjennom centroid av tverrsnitt.,

– Delen Modulus

Den maksimale bøyestyrke i en bredde er beregnet som σb = Mc / Ic, der c er avstanden fra nøytral aksen til den ekstreme fiber, Icis den centroidal treghetsmoment, og M er bøyemoment. Den delen modulus kombinerer c og Ic vilkårene i bøyestyrke ligningen:

ved Hjelp av den delen modulus, bøying stress er beregnet som σb = M / S. nytten av den delen modulus er at det preger bøyemotstand av et tverrsnitt i et enkelt begrep., Dette gir mulighet for optimalisering av en strålens tverrsnitt til å motstå bøye ved å maksimere en enkelt parameter.

Radius av Gyration

radius av gyration representerer avstanden fra et punkt er centroid som alle i området kan være konsentrert uten å ha noen effekt på treghetsmoment.,>

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration:

Egenskaper av Vanlige tverrsnitt

tabellen nedenfor gir egenskapene til vanlige tverrsnitt. Mer omfattende tabeller kan bli funnet i de nevnte referansene.

egenskaper som er beregnet i tabell inkluderer området, centroidal treghetsmoment, seksjon modulus, og radius av gyration.,

Notater

Merk 1: Nedbøyning på en Bjelke

utslag av en bjelke under bøying er bestemt av treghetsmoment av tverrsnitt, lengde, bredde, og den elastiske modulus av materialet. Mer detaljer er gitt i denne diskusjonen av strålen utslag.