Eine Nullhypothese ist eine genaue Aussage über eine Population, die wir mit Beispieldaten abzulehnen versuchen.Wir glauben normalerweise nicht, dass unsere Nullhypothese (oder H0) wahr ist. Wir benötigen jedoch eine genaue Aussage als Ausgangspunkt für statistische Signifikanztests.
Nullhypothese Beispiele
Oft-aber nicht immer – besagt die Nullhypothese, dass es keine Assoziation oder Differenz zwischen Variablen oder Unterpopulationen gibt., Wie so sind einige typische Nullhypothesen:
- die Korrelation zwischen Frustration und Aggression ist Null (Korrelationsanalyse);
- das Durchschnittseinkommen für Männer ist ähnlich dem für Frauen (unabhängige Stichproben t-Test);
- Nationalität ist (perfekt) unabhängig von der Musikpräferenz (Chi-Quadrat-Unabhängigkeitstest);
- Das durchschnittliche Bevölkerungseinkommen war über 2012 bis 2016 gleich (wiederholte Messungen ANOVA).
„Null“ Bedeutet nicht „Null“
Ein häufiges Missverständnis ist, dass „null“ „Null“impliziert. Dies ist oft, aber nicht immer der Fall., Zum Beispiel kann eine Nullhypothese auch sagen, dassDie Korrelation zwischen Frustration und Aggression ist 0.5.No null beteiligt hier und – wenn auch etwas ungewöhnlich-vollkommen gültig.
Die „Null“ in „Null-Hypothese“leitet sich von „nullify“ 5: die Null-Hypothese ist die Aussage, die wir zu widerlegen versuchen, unabhängig davon, ob es (nicht) einen Null-Effekt angeben.
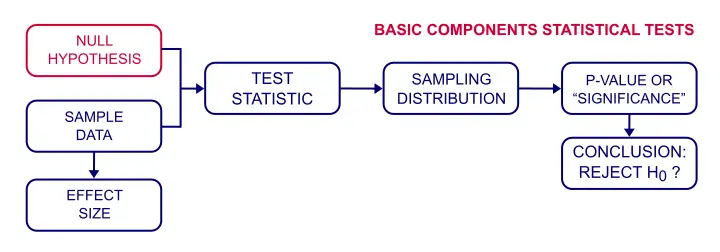
Null Hypothese testen-Wie funktioniert es?
ich will wissen, ob Glück ist verbunden mit Reichtum unter den Niederländer. Ein Ansatz, um dies herauszufinden, besteht darin, eine Nullhypothese zu formulieren., Da „verwandt mit“ nicht genau ist, wählen wir die entgegengesetzte Aussage als unsere Nullhypothese:Die Korrelation zwischen Reichtum und Glück ist bei allen Niederländern Null.Wir werden nun versuchen, diese Hypothese zu widerlegen, um zu zeigen, dass Glück und Reichtum in Ordnung sind.
Jetzt können wir nicht alle 17.142.066 Niederländer vernünftigerweise fragen, wie glücklich sie sich im Allgemeinen fühlen.

Also werden wir eine Stichprobe (sagen wir 100 Personen) nach ihrem Reichtum und ihrem Glück fragen. Die Korrelation zwischen Glück und Reichtum stellt sich in unserer Stichprobe als 0,25 heraus., Jetzt haben wir ein Problem: Die Ergebnisse der Stichproben unterscheiden sich tendenziell etwas von den Ergebnissen der Bevölkerung. Wenn also die Korrelation in unserer Population wirklich Null ist, finden wir möglicherweise eine Korrelation ungleich Null in unserer Stichprobe. Um diesen wichtigen Punkt zu veranschaulichen, schauen Sie sich das Scatterplot unten an. Es visualisiert eine Nullkorrelation zwischen Glück und Reichtum für eine gesamte Bevölkerung von N = 200.

Jetzt zeichnen wir eine Zufallsstichprobe von N = 20 aus dieser Population (die roten Punkte in unserem vorherigen Streudiagramm). Obwohl unsere Bevölkerungskorrelation Null ist, fanden wir eine erstaunliche 0.,82 korrelation in unserer Probe. Die folgende Abbildung veranschaulicht dies, indem alle nicht abgetasteten Einheiten aus unserem vorherigen Scatterplot weggelassen werden.

Dies wirft die Frage auf, wie wir jemals etwas über unsere Population sagen können, wenn wir nur eine winzige Stichprobe davon haben. Die grundlegende Antwort: Wir können selten etwas mit 100% iger Sicherheit sagen. Wir können jedoch mit 99%, 95% oder 90% Sicherheit viel sagen.
Wahrscheinlichkeit
Wie funktioniert das? Nun, im Grunde sind einige Beispielergebnisse angesichts unserer Nullhypothese höchst unwahrscheinlich., Die folgende Abbildung zeigt die Wahrscheinlichkeiten für verschiedene Stichprobenkorrelationen (N = 100), wenn die Populationskorrelation wirklich Null ist.

Ein Computer wird diese Wahrscheinlichkeiten leicht berechnen. Dies erfordert jedoch eine Stichprobengröße (in unserem Fall 100) und eine vermutete Populationskorrelation ρ (in unserem Fall 0). Deshalb brauchen wir eine Nullhypothese.
Wenn wir uns diese Stichprobenverteilung genau ansehen, sehen wir, dass Stichprobenkorrelationen um 0 am wahrscheinlichsten sind: Es besteht eine Wahrscheinlichkeit von 0,68, eine Korrelation zwischen -0,1 und 0,1 zu finden. Was bedeutet das?, Denken Sie daran, dass Wahrscheinlichkeiten als relative Frequenzen angesehen werden können. Stellen Sie sich also vor, wir würden 1.000 Proben zeichnen, anstatt die, die wir haben. Dies würde zu 1.000 Korrelationskoeffizienten führen, von denen etwa 680-eine relative Häufigkeit von 0,68 – im Bereich von -0,1 bis 0,1 liegen würden. Ebenso besteht eine Wahrscheinlichkeit von 0,95 (oder 95%), eine Stichprobenkorrelation zwischen -0,2 und 0,2 zu finden.
P-Werte
Wir fanden eine Beispielkorrelation von 0,25. Wie wahrscheinlich ist das, wenn die Bevölkerungskorrelation Null ist?, Die Antwort wird als p-Wert (kurz für Wahrscheinlichkeitswert) bezeichnet: Ein p-Wert ist die Wahrscheinlichkeit, ein Beispielergebnis zu finden, oder ein extremeres, wenn die Nullhypothese wahr ist.Angesichts unserer 0,25-Korrelation bedeutet“ extremer “ normalerweise größer als 0,25 oder kleiner als -0,25. Wir können aus unserer Grafik nicht sagen, aber die zugrunde liegende Tabelle sagt uns, dass p ≈ 0.012. Wenn die Nullhypothese wahr ist, besteht eine Wahrscheinlichkeit von 1,2%, unsere Stichprobenkorrelation zu finden.
Fazit?
Wenn unsere Populationskorrelation wirklich Null ist, können wir eine Stichprobenkorrelation von 0,25 in einer Stichprobe von N = 100 finden., Die Wahrscheinlichkeit, dass dies geschieht, beträgt nur 0,012, daher ist es sehr unwahrscheinlich. Eine vernünftige Schlussfolgerung ist, dass unsere Bevölkerungskorrelation schließlich nicht Null war.
Fazit: Wir lehnen die Nullhypothese ab. Angesichts unseres Stichprobenergebnisses glauben wir nicht mehr, dass Glück und Reichtum nichts miteinander zu tun haben. Wir können dies jedoch immer noch nicht mit Sicherheit sagen.
Nullhypothese-Einschränkungen
Bisher kamen wir nur zu dem Schluss, dass die Populationskorrelation wahrscheinlich nicht Null ist. Das ist die einzige Schlussfolgerung aus unserem Null-Hypothesen-Ansatz und es ist nicht wirklich so interessant.,
Was wir wirklich wissen wollen, ist, die Bevölkerung Korrelation. Unsere Probe Korrelation von 0,25 scheint eine vernünftige Schätzung. Wir nennen eine solche einzelne Zahl eine Punktschätzung.
Nun kann eine neue Probe mit einer anderen Korrelation kommen. Eine interessante Frage ist, wie stark unsere Stichprobenkorrelationen über Stichproben schwanken würden, wenn wir viele von ihnen zeichnen würden. Die folgende Abbildung zeigt genau das unter der Annahme unserer Stichprobengröße von N = 100 und unserer (Punkt -) Schätzung von 0,25 für die Populationskorrelation.,

Konfidenzintervalle
Unser Beispielergebnis legt nahe, dass etwa 95% vieler Proben eine Korrelation zwischen 0,06 und 0,43 aufweisen sollten. Dieser Bereich wird als Konfidenzintervall bezeichnet. Obwohl nicht genau richtig, ist es am einfachsten, als die Bandbreite zu bezeichnen, die wahrscheinlich die Populationskorrelation einschließen wird.
Eine Sache zu beachten ist, dass die concidence Intervall ist ziemlich breit. Es enthält fast eine Nullkorrelation, genau die Nullhypothese, die wir zuvor abgelehnt haben.,
Eine andere Sache zu beachten ist, dass unsere Probenahme Verteilung und Konfidenzintervall sind leicht asymmetrisch. Sie sind symmetrisch für die meisten anderen Statistiken (wie Mittel-oder Beta-Koeffizienten), aber keine Korrelationen.