Content-stałe przyspieszenie

Content

stałe przyspieszenie

wszyscy wiemy, że samochód przyspiesza, gdy położymy stopę na pedale przyspieszenia. Szybkość zmiany prędkości cząstki w stosunku do czasu nazywa się jej przyspieszeniem. Jeśli prędkość cząstki zmienia się ze stałą prędkością, to prędkość ta nazywa się stałym przyspieszeniem.,

na przykład, jeśli prędkość cząstki poruszającej się w linii prostej zmienia się równomiernie (ze stałą szybkością zmian) z 2 m/s do 5 m/s W ciągu jednej sekundy, to jej stałe przyspieszenie wynosi 3 m/s\(^2\).

zmniejszanie prędkości

Jeśli cząstka ma prędkość początkową 6 m/s i stałe przyspieszenie \(-2\) m/s\(^2\), to:

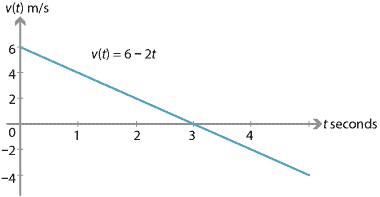
w ciągu pierwszych trzech sekund prędkość cząstki maleje (cząstka zwalnia). Po trzech sekundach cząstka jest chwilowo w spoczynku., Po trzech sekundach prędkość nadal maleje ,ale prędkość wzrasta (cząstka porusza się coraz szybciej).

podsumowanie

jeśli założymy, że szybkość zmiany prędkości (przyspieszenia) jest stała, to stałe przyspieszenie jest podane przez

\

dokładniej, stałe przyspieszenie \(a\) jest podane przez wzór

\

Gdzie \(v(t_i)\) jest prędkością w czasie \(t_i\). Ponieważ prędkość jest wektorem, tak samo przyspieszenie.,

wzory o stałym przyspieszeniu dla ruchu w linii prostej

w tym dziale rozważaliśmy ruch w linii prostej o stałym przyspieszeniu. Sytuacja ta jest bardzo powszechna; na przykład ciało poruszające się pod wpływem grawitacji podróżuje ze stałym przyspieszeniem.

przyjmuje się, że ruch rozpoczyna się, gdy \(t = 0\), a pozycja początkowa jest przyjmowana jako początek, czyli \(x(0) = 0\).,

pięć równań ruchu

1. \(v = U + at\)
2. \(x = \dfrac{(u+v)T}{2}\)
3. \(x = ut + \dfrac{1}{2}at^2\)
4. \(V^2 = U^2 + 2AX\)
5. \(x = VT – \dfrac{1}{2}at^2\)

uwaga. Każde z pięciu równań obejmuje cztery z pięciu zmiennych \(u, v, x, A, t\). Jeśli znane są wartości trzech zmiennych, to pozostałe wartości można znaleźć za pomocą dwóch równań.,

wzory o stałej akceleracji

pierwsze równanie ruchu

ponieważ przyspieszenie jest stałe, mamy \(a = \dfrac{v-U}{t}\). Daje to pierwsze równanie ruchu, \(v = U + at\).

drugie równanie ruchu

drugie równanie,

\

mówi, że przemieszczenie uzyskuje się przez pomnożenie średniej prędkości początkowej i końcowej przez czas, jaki upłynął podczas ruchu. Prościej:

\

możemy wyprowadzić to równanie używając faktu, że przemieszczenie jest równe podpisanemu obszarowi pod wykresem prędkości i czasu.,

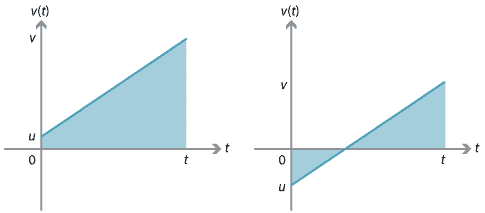
dla wykresu po prawej stronie, przemieszczenie można znaleźć, biorąc pod uwagę dwa trójkąty między wykresem a osią \(t\). Jeden z trójkątów ma dodatni obszar podpisany, a drugi ma ujemny obszar podpisany.

znalezienie przemieszczenia cząstki z wykresu Prędkość–Czas za pomocą integracji zostanie omówione w dalszej części tego modułu.,

trzecie równanie ruchu

zastępowanie \(v\) z pierwszego równania do drugiego równania daje

\begin{align*}x &= \dfrac{(U+v)T}{2} \ &= \ dfrac{(u+u+at)T}{2} \ \ &= \ dfrac{2UT+at^2}{2} \ \ &= ut + \ dfrac{1}{2}at^2, \end{align*}

które jest trzecim równaniem. Tak więc \(x\) jest kwadratem w \(t\), a zatem Wykres \(x\) przeciw \ (t\) jest parabolą.

czwarte równanie ruchu

z pierwszego równania mamy \(t = \dfrac{v-u}{a}\)., Podstawiając to do drugiego równania daje

\begin{align*}x &= \dfrac{(U+v)t}{2} \ &= \ dfrac{(U+v)(v-U)}{2A} \&= \ dfrac{V^2-U^2}{2a}. \end{align*}

przestawianie do \ (v^2\) podmiot tworzy czwarte równanie: \(v^2 = u^2 + 2ax\).

piąte równanie ruchu

z pierwszego równania mamy \(u = V-at\)., Używając drugiego równania, otrzymujemy

\begin{align*}x &= \dfrac{(u+V)T}{2} \ &= \ dfrac{(v-at+V)T}{2} \&= \ dfrac{2VT-at^2}{2} \ \&= VT- \ dfrac{1}{2}at^2, \ end{align*}

które jest piątym równaniem.

ruch pionowy

ruch spowodowany grawitacją jest dobrym kontekstem, w którym można zademonstrować zastosowanie wzorów o stałym przyspieszeniu., Jak wspomniano wcześniej, nasze dwa kierunki w ruchu pionowym są w górę iw dół, i należy podjąć decyzję, który z dwóch kierunków jest pozytywny. Przyspieszenie grawitacyjne jest stałą, o wielkości oznaczonej przez \(g\). W poniższym przykładzie przyjmujemy kierunek w górę, aby był dodatni i bierzemy \(g = 10\) m / s\(^2\).

dalsze korzystanie z równań ruchu

Next page – Content – Average velocity and average speed