funkcja Delta Diraca jest funkcją wprowadzoną w 1930 roku przez P. A. M. Diraca w jego przełomowej książce na temat mechaniki kwantowej. Model fizyczny, który wizualizuje funkcję delta, to rozkład masy skończonej masy całkowitej M-całki nad rozkładem masy., Gdy rozkład staje się coraz mniejszy, podczas gdy M jest stały, rozkład masy kurczy się do masy punktu, który z definicji ma zasięg zerowy, a jednak ma całkę o skończonej wartości równą masie całkowitej M. w granicy masy punktu rozkład staje się funkcją Diraca delta.
heurystycznie, funkcja Diraca delta może być postrzegana jako rozszerzenie delty Kroneckera z indeksów całkowych (elementów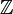 
) do indeksów rzeczywistych (elementów 
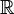)., Zauważ, że delta Kroneckera działa jako „filtr” w sumowaniu:
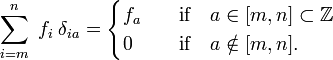
analogicznie, funkcja delta Diraca δ(x−a) jest zdefiniowana przez (Zastąp i przez x, a sumowanie nad i przez całkowanie nad x),
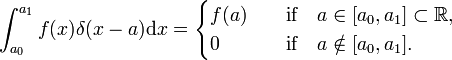
funkcja delta Diraca nie jest zwykłą dobrze zachowującą się mapą
div id=”D4efe881a0″>, ale Dystrybucja, znana również jako nieprawidłowa lub uogólniona funkcja. Fizycy wyrażają jej szczególny charakter stwierdzając, że funkcja delty Diraca ma sens jedynie jako czynnik w całce („pod całką”)., Matematycy twierdzą, że funkcja delta jest funkcją liniową na przestrzeni funkcji testowych.
spis treści
- 1 właściwości
- 2 ciągi Delta-zbieżne
- 2.1 funkcje blokowe
- 2.2 funkcje Gaussa
- 2.3 funkcje Lorentza-Cauchy ' ego
- 2.4 funkcje Sinc
- 3 pochodne funkcji deltal
- 3.,1 właściwości pochodnej
właściwości
najczęściej przyjmuje dolną i górną granicę w definicji funkcji delta równą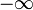 
I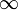 
, Od teraz to będzie zrobione.
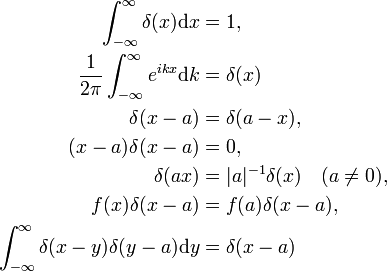
dowód fizyka tych właściwości przebiega przez wprowadzenie odpowiednich podstawień do całki i przy użyciu zwykłych zasad rachunku całkowego., Funkcja delta jako transformata Fouriera funkcji jednostkowej f (x) = 1 (druga właściwość) zostanie udowodniona poniżej. Ostatnia właściwość jest analogią mnożenia dwóch macierzy tożsamości,
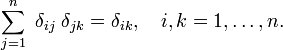
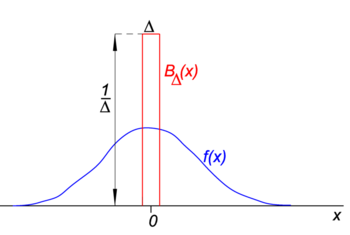
Fig. 1. Block („boxcar”) function (red) times regular function f (x) (blue).
sekwencje Delta-zbieżne
istnieją rodziny funkcji regularnych Fa(x), których członkowie rodziny różnią się wartością pojedynczego parametru α., Przykładem takiej rodziny jest rodzina funkcji Gaussa FA (x) = exp (−ax2), gdzie różne wartości pojedynczego parametru α wyróżniają poszczególne człony. Gdy wszystkie człony są liniowo unormowalne, tzn. następująca Całka jest skończona niezależnie od α,
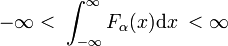
i wszystkie człony są szczytowe wokół x = 0, to rodzina może tworzyć ciąg Delta-zbieżny.,
funkcje blokowe
najprostszym przykładem sekwencji Delta-zbieżnej jest rodzina funkcji blokowych, charakteryzująca się dodatnim Δ,
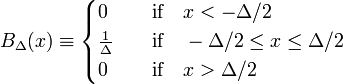
na Rys. 1 funkcja blokowa BΔ jest pokazana na Czerwono. Widocznie pole (szerokość razy wysokość) pod czerwoną krzywą jest równe jedności, niezależnie od wartości Δ,
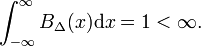
niech Funkcja Dowolna f(x) (niebieski na Rys. 1) być ciągłym (bez skoków) i skończonym w sąsiedztwie x=0., Gdy Δ staje się bardzo mała, a funkcja blokowa bardzo wąska (i koniecznie bardzo wysoka, ponieważ szerokość razy wysokość jest stała), iloczyn f (x) BΔ(x) staje się w dobrym przybliżeniu równy f(0) BΔ(x). Im węższy blok, tym lepsze przybliżenie., Dlatego dla Δ ID = „11a2406a83” >
które mogą być porównane z definicją funkcji delta,
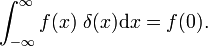
pokazuje to, że rodzina funkcji blokowych zbieżna jest do funkcji delta Diraca dla zmniejszenia parametru Δ; rodzina tworzy ciąg zbieżny delta:
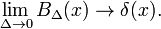
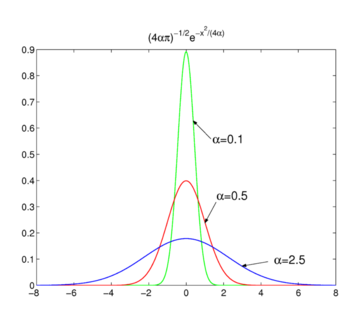
rys. 2. Funkcje Gaussa.
Uwaga: zintegrowaliśmy całą rzeczywistą oś., Oczywiście nie jest to konieczne, mogliśmy wykluczyć zerowe skrzydła funkcji blokowej i zintegrować tylko nad garb w środku, od-Δ/2 do + Δ / 2. W tekstach matematycznych, jak np. Ref. , to udoskonalenie granic całkowania zawarte jest w definicji sekwencji Delta-zbieżnej. Oznacza to, że wymagane jest, aby całki nad dwoma skrzydłami zniknęły w granicy. Ponieważ ciągi Delta-zbieżne spotykane w zastosowaniach fizycznych zazwyczaj spełniają ten warunek, pomijamy dokładniejszą definicję matematyczną.,
funkcje Gaussa
rozważmy rodzinę,
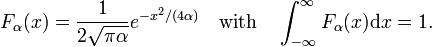
jak pokazano na Rys. 2 funkcje szczytowe wokół x = 0 i stają się węższe dla zmniejszenia α. Dlatego rodzina funkcji Gaussa tworzy ciąg zbieżny delta,
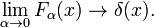
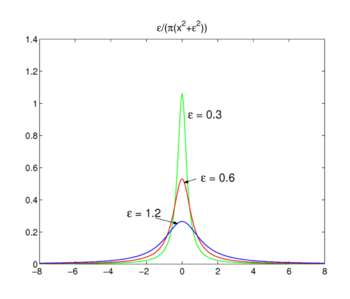
Fig. 3. Funkcje Lorentza-Cauchy 'ego
funkcje Lorentza-Cauchy' ego
rodzina funkcji pokazana na Rys., 3
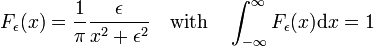
forms a delta-convergent sequence,
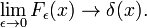
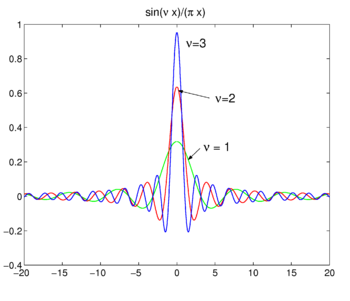
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 jest
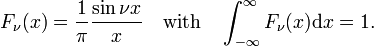
ta rodzina łączy się z funkcją delta dla zwiększenia ν
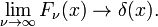
ta granica prowadzi łatwo do Całkowej reprezentacji Fouriera funkcji delta:
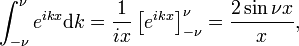
tak, że
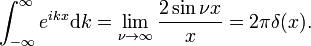
funkcja Diraca delta jest transformatą Fouriera funkcji jednostkowej F(x) = 1.
pochodne funkcji delta
rozważ różniczkowalną funkcję f(x), która znika w nieskończoności plus i minus.,d=”ed7dae11d6″>
w ten sam sposób, w jaki udowadnia się regułę obrotu i Hermityczność kwantowego mechanicznego operatora pędu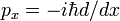 
, pokazaliśmy tutaj, że D/dx jest anty-Hermityzmem,
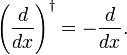
rzeczywiście, kiedy piszemy całkę jako produkt wewnętrzny, wynika to z częściowej integracji i znikanie F(X) na granicach całkowania, które
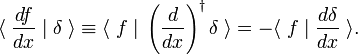
ta reguła obrotu jest używana jako definicja pochodnej funkcji Delta,
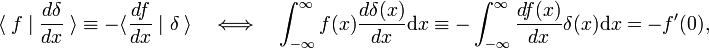
gdzie pierwsza oznacza pierwszą pochodną F(X)., Zgodnie z definicją funkcji delta pierwsza pochodna jest oceniana w x = 0. Używając m razy reguły obrotu, wynika z tego, że M −ta pochodna funkcji delta jest zdefiniowana przez
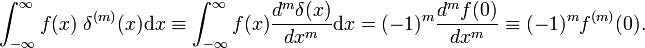
właściwości pochodnej
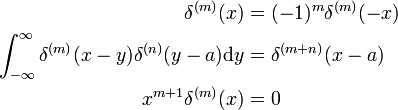
wyniki te można udowodnić poprzez podstawienie X → – X i użycie reguły obrotu dla d/dx (patrz wyżej).,
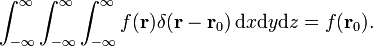
trójwymiarowa funkcja delta może być faktoryzowana
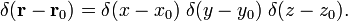
we współrzędnych biegunowych sferycznych
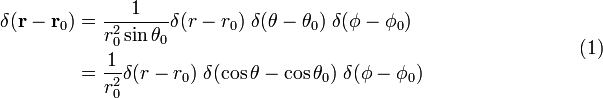
dowód równania (1)
napisz
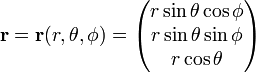
jakobian (wyznacznik Jacobiego) tej transformacji ze współrzędnych kartezjańskich do współrzędnych biegunowych sferycznych jest
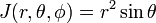
rozważ
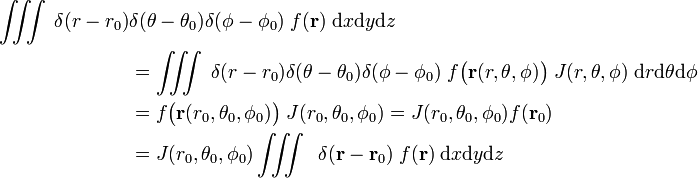
tak, że
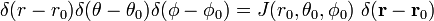
i
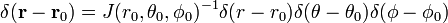
ostatnia linia równania (1) wynika z reguły łańcucha.,
poniżej przedstawiono użyteczną i często stosowaną właściwość,
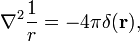
gdzie ∇2 jest operatorem Laplace ' a w trójwymiarowych współrzędnych kartezjańskich, A R jest długością r.