funkcje logarytmiczne są odwrotnościami funkcji wykładniczych. Odwrotnością funkcji wykładniczej y = ax jest x = ay. Funkcja logarytmiczna y = logax jest zdefiniowana jako równoważna równaniu wykładniczemu x = ay. y = logax tylko w następujących warunkach: x = ay, a > 0, a≠1. Nazywa się ją funkcją logarytmiczną z bazą a.
zastanów się, co oznacza odwrotność funkcji wykładniczej: x = ay., Biorąc pod uwagę liczbę x i bazę a, do jakiej potęgi y musi być podniesione do równej x? Ten nieznany wykładnik, y, równa się logax. Więc widzisz logarytm jest niczym więcej niż wykładnikiem. Z definicji, alogax = x, dla każdego rzeczywistego x > 0.
Poniżej znajdują się wykresy postaci y = logax, gdy a> 1 i gdy 0< a< 1. Zauważ, że dziedzina składa się tylko z dodatnich liczb rzeczywistych i że funkcja zawsze rośnie wraz ze wzrostem x.,
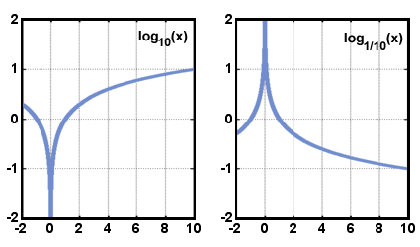
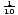 x.
x.domeną funkcji logarytmicznej są liczby rzeczywiste większe od zera, A Zakres to liczby rzeczywiste. Wykres y = logax jest symetryczny do wykresu y = ax w odniesieniu do linii y = x. zależność ta jest prawdziwa dla dowolnej funkcji i jej odwrotności.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(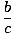 ) = logab – logac., ) = logab – logac., |
| loga(XD) = d logax |
naturalna funkcja logarytmiczna jest funkcją logarytmiczną o podstawie E. F (X) = logex = LN X, gdzie x > 0. ln x jest tylko nową formą notacji dla logarytmów z bazą e. Większość kalkulatorów ma przyciski oznaczone ” log ” i „ln”. Przycisk „log” zakłada, że baza jest dziesięć, a przycisk „ln”, oczywiście, pozwala na bazę równą e., Funkcja logarytmiczna z bazą 10 jest czasami nazywana wspólną funkcją logarytmiczną. Jest szeroko stosowany, ponieważ nasz system numeracji ma bazę dziesięć. Logarytmy naturalne są częściej spotykane w rachunku różniczkowym.
istnieją dwie formuły, które pozwalają na zmianę podstawy funkcji logarytmicznej. Pierwszy z nich mówi tak: logab = 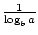 . Bardziej znany i użyteczny wzór na zmianę BAZ jest powszechnie nazywany zmianą formuły bazowej. Pozwala na zmianę podstawy funkcji logarytmicznej na dowolną dodatnią liczbę rzeczywistą ≠1. Stwierdza, że logax =
. Bardziej znany i użyteczny wzór na zmianę BAZ jest powszechnie nazywany zmianą formuły bazowej. Pozwala na zmianę podstawy funkcji logarytmicznej na dowolną dodatnią liczbę rzeczywistą ≠1. Stwierdza, że logax = 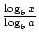 ., W tym przypadku a, b i x są dodatnimi liczbami rzeczywistymi, a a, B≠1.
., W tym przypadku a, b i x są dodatnimi liczbami rzeczywistymi, a a, B≠1.
w następnej sekcji omówimy niektóre zastosowania funkcji wykładniczych i logarytmicznych.