hipoteza zerowa jest precyzyjne stwierdzenie o populacji, że staramy się odrzucić z danych próbki.Zwykle nie wierzymy, że nasza hipoteza zerowa (lub H0) jest prawdziwa. Potrzebujemy jednak dokładnego oświadczenia jako punktu wyjścia do badania istotności statystycznej.
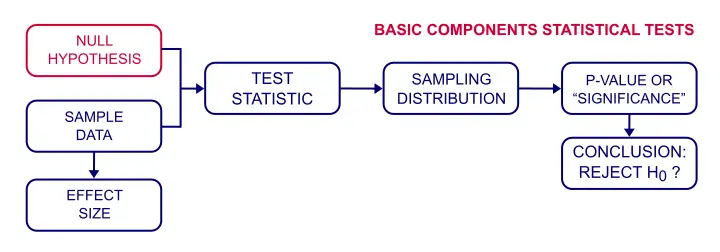
przykłady hipotezy zerowej
często – ale nie zawsze-hipoteza zerowa stwierdza, że nie ma związku lub różnicy między zmiennymi lub subpopulacji., Podobnie, niektóre typowe hipotezy zerowe to:
- korelacja między frustracją a agresją jest zerowa (analiza korelacji);
- średni dochód dla mężczyzn jest podobny do tego dla kobiet (niezależne próbki t-test);
- narodowość jest (całkowicie) niezwiązana z preferencjami muzycznymi (test niezależności chi-kwadrat);
- średni dochód populacji był równy w latach 2012-2016 (powtarzane miary ANOVA).
„Null” nie oznacza „Zero”
powszechnym nieporozumieniem jest to, że „null” oznacza „zero”. Tak jest często, ale nie zawsze., Na przykład hipoteza zerowa może również stwierdzać, że korelacja między frustracją a agresją jest 0.5.No zero tu zaangażowane i – choć dość nietypowe-doskonale uzasadnione.
„null” w „hipoteza zerowa” wynika z „nullify”5: hipoteza zerowa jest stwierdzenie, że staramy się obalić, niezależnie od tego, czy Nie (Nie) określić zerowy efekt.
Testowanie hipotezy zerowej – Jak to działa?
chcę wiedzieć, czy szczęście jest związane z bogactwem wśród Holendrów. Jednym z podejść do tego jest sformułowanie hipotezy zerowej., Ponieważ „powiązane” nie jest precyzyjne, wybieramy przeciwne stwierdzenie jako naszą hipotezę zerową:korelacja między bogactwem a szczęściem jest zerowa wśród wszystkich Holendrów.Spróbujemy teraz obalić tę hipotezę, aby pokazać, że szczęście i bogactwo są ze sobą powiązane.
Teraz nie możemy zapytać wszystkich 17.142.066 Holendrów, jak się ogólnie czują szczęśliwi.

więc zapytamy próbkę (powiedzmy 100 osób) o ich bogactwo i szczęście. Korelacja między szczęściem a bogactwem okazuje się mieć wartość 0,25 w naszej próbie., Teraz mamy jeden problem: wyniki prób różnią się nieco od wyników populacji. Więc jeśli korelacja naprawdę jest zerowa w naszej populacji, możemy znaleźć niezerową korelację w naszej próbie. Aby zilustrować ten ważny punkt, spójrz na punkt poniżej. Wizualizuje zerową korelację między szczęściem a bogactwem dla całej populacji N = 200.

teraz losujemy losową próbkę N = 20 z tej populacji (czerwone kropki w naszym poprzednim punkcie). Mimo że nasza korelacja populacji wynosi zero, znaleźliśmy oszałamiające 0.,82 korelacja w naszej próbce. Poniższy rysunek ilustruje to, pomijając wszystkie jednostki nieobjęte próbą z naszego poprzedniego scatterplot.

to rodzi pytanie, jak możemy kiedykolwiek powiedzieć cokolwiek o naszej populacji, jeśli mamy tylko małą próbkę z niego. Podstawowa odpowiedź: rzadko możemy powiedzieć cokolwiek ze 100% pewnością. Możemy jednak powiedzieć wiele z 99%, 95% lub 90% pewnością.
prawdopodobieństwo
Jak to działa? Cóż, w zasadzie, niektóre przykładowe wyniki są mało prawdopodobne biorąc pod uwagę naszą hipotezę zerową., Jak tak, poniższy rysunek pokazuje prawdopodobieństwa dla różnych korelacji próbki (N = 100), jeśli korelacja populacji naprawdę jest zero.

komputer z łatwością wyliczy te prawdopodobieństwa. Wymaga to jednak wielkości próby (100 w naszym przypadku) i domniemanej korelacji populacji ρ (0 w naszym przypadku). Dlatego potrzebujemy hipotezy zerowej.
jeśli przyjrzymy się dokładnie rozkładowi próbkowania, zobaczymy, że korelacje próbki wokół 0 są najbardziej prawdopodobne: istnieje prawdopodobieństwo 0,68 znalezienia korelacji między -0,1 i 0,1. Co to znaczy?, Cóż, pamiętaj, że prawdopodobieństwo może być postrzegane jako względne częstotliwości. Wyobraź sobie, że pobierzemy 1000 próbek zamiast tej, którą mamy. Wynikałoby to z 1000 współczynników korelacji, a około 680 z nich – o względnej częstotliwości 0,68-mieściłoby się w zakresie od -0,1 do 0,1. Podobnie, istnieje 0.95 (lub 95%) prawdopodobieństwo znalezienia próbki korelacji między -0.2 i 0.2.
wartości P
znaleźliśmy przykładową korelację 0,25. Jak prawdopodobne jest to, że korelacja populacji wynosi zero?, Odpowiedź jest znana jako wartość p(skrót od wartości prawdopodobieństwa): wartość p jest prawdopodobieństwo znalezienia jakiegoś wyniku próbki lub bardziej ekstremalne, jeśli hipoteza zerowa jest prawdziwa.Biorąc pod uwagę naszą korelację 0.25 ,” bardziej ekstremalne ” zwykle oznacza większe niż 0.25 lub mniejsze niż -0.25. Nie możemy stwierdzić z naszego wykresu, ale tabela bazowa mówi nam, że p ≈ 0.012. Jeśli hipoteza zerowa jest prawdziwa, istnieje 1.2% prawdopodobieństwo znalezienia naszej korelacji próbki.
wniosek?
Jeśli nasza korelacja populacyjna naprawdę wynosi zero, to w próbce N = 100 możemy znaleźć korelację próbną równą 0,25., Prawdopodobieństwo tego zdarzenia wynosi tylko 0,012, więc jest to bardzo mało prawdopodobne. Rozsądnym wnioskiem jest to, że nasza korelacja populacji nie była jednak zerowa.
wniosek: odrzucamy hipotezę zerową. Biorąc pod uwagę nasz przykładowy wynik, nie wierzymy już, że szczęście i bogactwo nie są ze sobą powiązane. Jednak nadal nie możemy stwierdzić tego z całą pewnością.
hipoteza zerowa-ograniczenia
do tej pory doszliśmy tylko do wniosku, że korelacja populacji prawdopodobnie nie jest zerowa. To jedyny wniosek z naszego podejścia hipotezy zerowej i nie jest to naprawdę interesujące.,
to co naprawdę chcemy wiedzieć to korelacja populacji. Nasza przykładowa korelacja 0.25 wydaje się rozsądnym oszacowaniem. Taką liczbę nazywamy oszacowaniem punktowym.
Teraz nowa próbka może pochodzić z innej korelacji. Ciekawym pytaniem jest, jak bardzo nasze korelacje próbek będą się wahać w stosunku do próbek, gdybyśmy narysowali wiele z nich. Poniższy rysunek pokazuje dokładnie, że przy założeniu naszej wielkości próby N = 100 i naszego (punktowego) oszacowania 0,25 dla korelacji populacji.,

przedziały ufności
Nasz wynik próby sugeruje, że około 95% wielu próbek powinno znaleźć korelację między 0,06 A 0,43. Zakres ten jest znany jako przedział ufności. Chociaż nie jest to dokładnie poprawne, najłatwiej jest jednak o przepustowość, która prawdopodobnie zamknie korelację populacji.
należy zauważyć, że przedział osiadania jest dość szeroki. Prawie zawiera zerową korelację, dokładnie hipotezę zerową, którą odrzuciliśmy wcześniej.,
kolejną rzeczą do zauważenia jest to, że nasz rozkład próbkowania i przedział ufności są nieco asymetryczne. Są one symetryczne dla większości innych statystyk (takich jak środki lub współczynniki beta), ale nie korelacje.