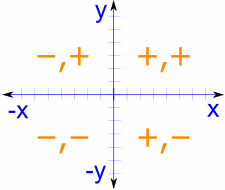
„Jednostka okrąg” jest okręgiem o promieniu 1.
jest tak prosty, że jest to świetny sposób, aby nauczyć się i porozmawiać o długościach i kątach.
środek jest umieszczony na wykresie, na którym krzyżują się oś x i oś y, więc otrzymujemy tutaj taki schludny układ.

Sinus, Cosinus i tangens
ponieważ promień wynosi 1, możemy bezpośrednio mierzyć sinus, cosinus i tangens.,

Co się dzieje, gdy kąt θ wynosi 0°?
cos 0° = 1, sin 0° = 0 and tan 0° = 0
Co się dzieje, gdy θ wynosi 90°?
cos 90° = 0, sin 90° = 1 and tan 90° is undefined
Wypróbuj Sam!
spróbuj!, Przesuń mysz, aby zobaczyć, jak różne kąty (w radianach lub stopniach) wpływają na sinus, cosinus i tangens
„boki” mogą być dodatnie lub ujemne zgodnie z zasadami współrzędnych kartezjańskich. To sprawia, że sinus, cosinus i styczna zmiana między dodatnimi i ujemnymi wartościami również.
wypróbuj również interaktywne koło jednostek.,
Twierdzenie Pitagorasa
twierdzenie Pitagorasa mówi, że dla trójkąta prostokątnego kwadrat długiego boku jest równy sumie kwadratów trójkąta prostokątnego.inne dwie strony:
x2 + y2 = 12
ale 12 to tylko 1, więc:
x2 + y2 = 1
(równanie okręgu jednostkowego)
również, ponieważ x=cos I y=sin, otrzymujemy:
(cos(θ))2 + (Sin(θ))2 = 1
użyteczna „tożsamość”
ważna kąty: 30°, 45° i 60°
należy starać się zapamiętać sin, cos I TAN dla kątów 30°, 45° i 60°.,
tak, tak, to ból, aby pamiętać rzeczy, ale ułatwi życie, gdy je znasz, nie tylko na egzaminach, ale innym razem, gdy trzeba zrobić szybkie szacunki itp.
to są wartości, o których powinieneś pamiętać!,id=”0f47f3223b”>
What about tan?,
cóż, tan = sin/cos, więc możemy to obliczyć tak:
tan(30°) =sin(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sin (45°)cos(45°) = √2/2√2/2 = 1
tan(60°) =sin (60°)cos(60°) = √3/21/2 = √3
* Uwaga: zapisanie 1√3 może kosztować znaki (Patrz racjonalne mianowniki), więc zamiast tego użyj √33
szybki szkic
innym sposobem, aby pomóc Ci zapamiętać 30° i 60°, jest szybkie szkicowanie:
| narysuj trójkąt o długości boków 2 | 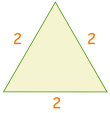 |
|
|
przeciąć na pół.,div id=”56c966b492″> przykład: sin(30°)Sinus: sohcahtoa sinus jest przeciwny podzielony przez przeciwprostokątną
sin(30°) = oppositehypotenuse = 12
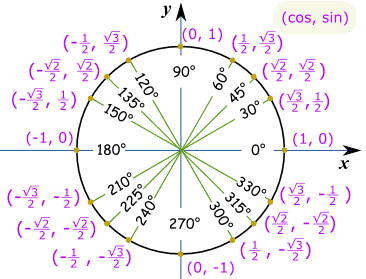
cały okrągdla całego okręgu potrzebujemy wartości w każdym kwadrancie, z prawidłowym znakiem plus lub minus według współrzędnych kartezjańskich: zauważ, że cos jest pierwszy, a sin jest drugi, więc idzie (cos, sin): div
Articles
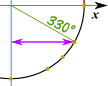
Zapisz jako PDF przykład: co to jest cos(330°) ?,
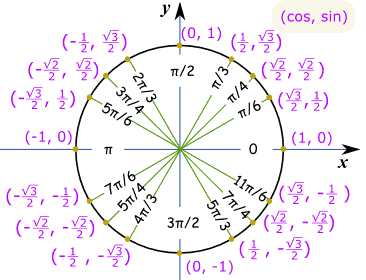
zrób szkic w ten sposób, a widzimy, że jest to „długa” wartość: √32 i jest to ten sam okrąg jednostki w radianach.
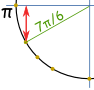
przykład: czym jest grzech(7π/6) ?
pomyśl „7π/6 = π + π/6”, a następnie zrób szkic. widzimy wtedy, że jest ujemna i jest „krótka” wartość − – ½ |