na tych stronach przyjrzymy się kilku ciekawym pojęciom, spojrzymy na przestrzeń zakrzywioną: co oznacza przestrzeń zakrzywiona, jak możemy stwierdzić, czy przestrzeń jest zakrzywiona z wewnątrz czy z zewnątrz.
patrzymy na to, jak możemy osadzić rodzaj przestrzeni wewnątrz innego i widzimy, że możemy mapować między różnymi przestrzeniami na różne sposoby.
przyglądamy się też zagęszczeniu i temu, jak możemy reprezentować nieskończenie duże i nieskończenie małe wektory w naszych przestrzeniach w sposób, który nie prowadzi do osobliwości i innych problemów.,
pojęcia te okazują się przydatne, nawet gdy pracujemy z przestrzenią płaską, znajdziemy sposoby na reprezentowanie wektorów i płaszczyzn, które nie przechodzą przez początek. Daje nam to sposoby przedstawiania rotacji i tłumaczeń jako jednej operacji.
druga aplikacja jest relatywistyczna czasoprzestrzeń.
Geometria Rienmannowska
w geometrii Rienmannowskiej przestrzeń może być krzywa w różnych miejscach (patrz Rozmaitości) tutaj patrzymy na geometrie, w których krzywa przestrzeni jest stała.,
Geometria Eulidean
przestrzeń płaska
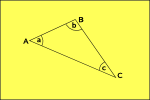
Geometria hiperboliczna
krzywe przestrzeni na zewnątrz
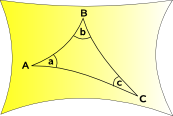
geometria sferyczna i eliptyczna
krzywe przestrzeni do wewnątrz
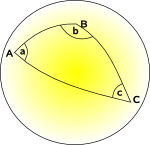
w geometrii zakrzywionej (nie-euklidesowej) nie możemy znaleźć zestawu współrzędnych, które są wzajemnie prostopadłe, gdzie wszystkie linie współrzędnych są równoległe do siebie i gdzie każdy kwadrat siatki ma ten sam obszar., Możemy znaleźć układ współrzędnych, w którym możemy wykonać niektóre z nich, ale nie wszystkie.
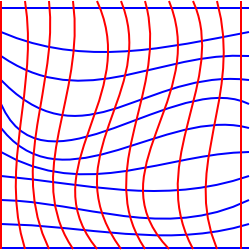
ten diagram stara się zilustrować tę sytuację w 2 wymiarach, chociaż jest nieco mylące, ponieważ narysowaliśmy go na płaszczyźnie, więc mogliśmy narysować współrzędne prostokątne.
aby zilustrować sytuację, w której jest to niemożliwe, moglibyśmy pomyśleć o dwuwymiarowej płaszczyźnie, która została rozciągnięta do trzeciego wymiaru.,

w tej sytuacji możemy wybrać współrzędne, które tworzą prostokątną siatkę po rzutowaniu na płaszczyznę poziomą, jednak dla osoby mieszkającej na powierzchni niektóre kwadraty siatki będą wyglądać na większe niż inne, a linie siatki mogą nie wyglądać na równoległe. Nie ma dwuwymiarowego układu współrzędnych, który zachowałby równoległe linie, kąty i obszary jednocześnie.,
podobnym przykładem jest próba odwzorowania powierzchni Ziemi, możemy użyć linii szerokości i długości geograficznej, ale linie długości geograficznej zbliżają się bliżej biegunów.
w takich przypadkach możemy pracować w zakresie współrzędnych trójwymiarowych i takie podejście przyjmiemy z niektórymi rodzajami geometrii Nieeuklidesowych. Często możliwe jest osadzenie określonej geometrii w Wyższej geometrii wymiarowej, aby uczynić ją bardziej euklidesową.,
czasami zdarza się, że gdy patrzymy na geometrię w dużej skali, to jest ona nie-euklidesowa, ale jeśli patrzymy na nią w coraz mniejszej skali, to przybliża się do geometrii euklidesowej. Aby to zrobić, musimy znaleźć układ współrzędnych, w którym kąty są zachowane w każdym punkcie, to znaczy, poziome i pionowe linie współrzędnych muszą zawsze przecinać się pod kątem 90°, nawet jeśli linie mogą nie być proste. Jest to tzw. geometria konforemna. W tego typu geometrii możemy przynajmniej zdefiniować lokalny układ współrzędnych.,
związane z tym jest to, czy geometria może być zróżnicowana i zintegrowana, warunkiem jest to, że musi być dobrze zachowana i nie ma żadnych nagłych skoków itp. Niektóre geometrie i układy współrzędnych mogą być dobrze zachowane w niektórych miejscach, ale mają osobliwości itp.
dyskusja na temat pomiaru krzywizny znajduje się na tej stronie.
notacja matematyczna
Jak radzić sobie z geometriami, gdzie nie możemy użyć wszystkich reguł, które mają zastosowanie do geometrii euklidesowej?,
jednym z podejść jest użycie notacji tensorowej, to dostarcza konwencje i notacje, które pomagają nam w przełączaniu między różnymi układami współrzędnych. Ortogonalny układ współrzędnych, lokalny do dowolnego punktu, można zdefiniować za pomocą wektorów bazowych, które są stycznymi do linii współrzędnych.,Kolektor
zobacz tę stronę
relacja między geometriami Hiperbolicznymi i Minkowskiego
| Geometria Minkowskiego | Geometria hiperboliczna | |
| punkt | Zdarzenie w czasie przestrzeni | cząstka w ruchu jednorodnym |
| odległość między dwoma punktami | czasoprzestrzeń między dwoma zdarzeniami | względna prędkość między dwoma takimi cząstkami |
terminologia
tutaj przyjrzymy się terminologii, takiej jak geometrie, przestrzenie, modele, rzuty i transformaty., Jest to dość trudne, gdy zaczynamy zajmować się geometriami nie-Euklidesowymi, ponieważ używamy podobnej terminologii, do której jesteśmy przyzwyczajeni w konwencjonalnej przestrzeni euklidesowej, ale terminy mogą mieć nieco inne właściwości.,spróbuj
Geometria eliptyczna
modele
przykłady to:
- górna połowa-model płaszczyzny
- model dysku Poincarego
- model projekcyjny
- model konformalny
projekcje
projekcje stereograficzne
transformaty
niezmienne
przykłady to:
- transformata Möbiusa
- transformata Lorentza
transformata równoległa postulat
jeśli usuniemy postulat równoległy z przestrzeni euklidesowej.,
prowadzi to do:
- postulat równoległy jest false
- kąty trójkąta nie dodają się do π
- dla kształtu o danej wielkości, w ogóle nie istnieje podobny kształt o większej wielkości.,ктив
conformal (dysk Poincare ) proste linie – ортодромии segmentów okręgów kąt zapisz kąty wewnętrzne trójkąta π-(α+β+γ)=CΔ odległość między dwoma punktami z