rozwiązuj równania numerycznie

Znajdź wszystkie korzenie funkcji wielomianowej

użyj vpasolve aby znaleźć wszystkie rozwiązania funkcji f(x)=6X7-2×6+3×3-8.

syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)

vpasolve zwraca siedem korzeni funkcji, zgodnie z oczekiwaniami, ponieważ funkcja jest wielomianem stopnia siódmego.,

Znajdź zera funkcji Niepolynomicznej za pomocą zakresów wyszukiwania i punktów początkowych

wykres funkcji f(x)=e(x / 7)cos(2x) ujawnia okresowe zera, ze wzrostem nachylenia w punktach zerowych w miarę wzrostu x.

syms xh = fplot(exp(x/7)*cos(2*x),);grid on

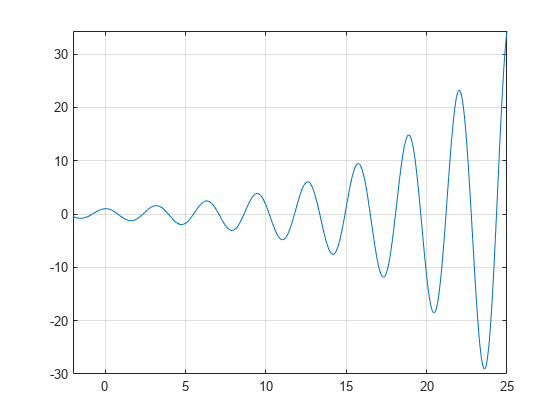
użyjvpasolveaby znaleźć zero funkcjif. Zauważ, że vpasolve zwraca tylko jedno rozwiązanie równania niepolynomialnego, nawet jeśli istnieje wiele rozwiązań., On repeated calls, vpasolve returns the same result.

f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.

for k = 1:3 vpasolve(f,x,'Random',true)end

ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')

ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')

ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')

To find a zero close to x=10, set the starting point to 10.,

vpasolve(f,x,10)

ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')

vpasolve(f,x,1000)

ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')

vpasolve(f,x,)

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

aby znaleźć wiele zer w zakresie , nie można wywoływać vpasolve wielokrotnie, ponieważ zwraca ten sam wynik przy każdym wywołaniu, jak poprzednio pokazano. Zamiast tego ustaw zakres wyszukiwania i ustaw 'Random' na true.,

for k = 1:3 vpasolve(f,x,,'Random',true)end

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')

ponieważ 'Random' i wybiera punkt wyjścia w losowej kolejności, to samo rozwiązanie można znaleźć na kolejne wyzwania.,

Znajdź wszystkie zera w określonym zakresie wyszukiwania

Utwórz funkcjęfindzeros aby systematycznie znajdować wszystkie zera dlaf w określonym zakresie wyszukiwania, z określoną tolerancją błędów. Funkcja rozpoczyna się od zakresu wyszukiwania wejściowego i wywołuje vpasolve, aby znaleźć zero. Następnie dzieli zakres wyszukiwania na dwa wokół wartości zero i rekurencyjnie wywołuje się z nowymi zakresami wyszukiwania jako wejściami, aby znaleźć więcej zer.

funkcja jest wyjaśniona sekcja po sekcji tutaj.,

deklaruje funkcję z trzema wejściami i Jednym Wyjściem. Pierwsze wejście to funkcja, drugie wejście to Zakres, a opcjonalne trzecie wejście pozwala określić błąd pomiędzy zerem a generowanymi z niego wyższymi i niższymi granicami.

function sol = findzeros(f,range,err)

Jeśli nie podasz opcjonalnego argumentu tolerancji błędów,findzeros ustawiaerr na0.001.

if nargin < 2 err = 1e-3;end

Znajdź zero w zakresie wyszukiwania za pomocąvpasolve.,

sol = vpasolve(f,range);

Jeślivpasolve nie znajdzie zera, kończy działanie.

if(isempty(sol)) return

Jeślivpasolve znajdzie zero, podziel zakres wyszukiwania na dwa zakresy wyszukiwania powyżej i poniżej zera.

else lowLimit = sol-err; highLimit = sol+err;

wywołajfindzeros z dolnym zakresem wyszukiwania. Jeśli findzeros zwróci zera, skopiuj wartości do tablicy rozwiązania i posortuj je.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end

wywołajfindzeros z wyższym zakresem wyszukiwania., Jeśli findzeros zwróci zera, skopiuj wartości do tablicy rozwiązania i posortuj je.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend

cała funkcjafindzeros jest następująca. Zapisz tę funkcję jako findzeros.m w bieżącym folderze.

syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'

uzyskaj rozwiązania z dowolną precyzją

użyjdigits aby ustawić precyzję rozwiązań zwracanych przezvpasolve., Domyślnie vpasolve zwraca rozwiązania z dokładnością do 32 cyfr znaczących.

f = exp(x/7)*cos(2*x);vpasolve(f)

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

użyj digits aby zwiększyć dokładność do 64 cyfr znaczących. Podczas modyfikowania digits upewnij się, że zapisałeś jego bieżącą wartość, aby móc ją przywrócić.,

digitsOld = digits;digits(64)vpasolve(f)

ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')

następnie zmień dokładność rozwiązań na 16 znaczących liczb.

digits(16)

rozwiązuj równania wielowymiarowe za pomocą zakresów wyszukiwania

rozważ następujący układ równań.

Wykres równań dla 0≤x≤2.5 i 0≤x≤2.5 pokazuje, że trzy powierzchnie przecinają się w dwóch punktach., Aby lepiej zobrazować Wykres, użyj view. Aby przeskalować wartości colormap, użyj caxis.

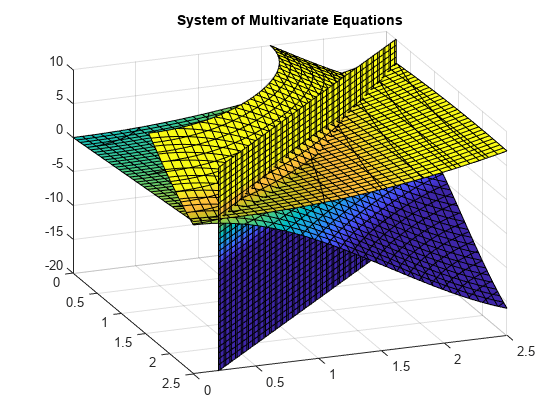
użyjvpasolve aby znaleźć punkt, w którym przecinają się powierzchnie. Funkcja vpasolve zwraca strukturę. Aby uzyskać dostęp do x-, y – I z-wartości rozwiązania, indeksuj do struktury.,

sol = vpasolve(equations);

vars = ;range = ;sol = vpasolve(equations, vars, range);

digits(digitsOld)