
Czy zastanawiałeś się kiedyś jak może padać śnieg w above freezing temperature? Cóż, naiwnym wyjaśnieniem jest to, że po prostu potrzeba czasu, aby płatki śniegu stopiły się, gdy przenikną nad zamarzającym powietrzem, gdy opadają w dół do ziemi. To jest oczywiście powód, dla którego Grad może spaść w ciepłe dni. Po prostu kamienie gradu spadają szybko, zbyt szybko, aby ciepłe powietrze stopiło Grad. Nie jest to jednak główne wyjaśnienie, dlaczego może padać śnieg, Gdy jest powyżej mrozu.,
z poniższego rysunku wynika, że istnieje wyraźna zależność od wilgotności-im jest sucha, tym cieplej może być podczas śniegu. Oznacza to, że główny czynnik, przynajmniej w suchych warunkach, ma związek z wilgotnością. A tym czynnikiem jest parowanie. Dokładniej, gdy opadają płatki śniegu, wyparowują. Proces ten pobiera ciepło i utrzymuje płatki na zimno.
tak więc, jeśli chcemy obliczyć temperaturę maksymalną, musimy oszacować bilans cieplny netto płatka. Po pierwsze, gdy płatki podróżują w ciepłym otoczeniu, zyskują ciepło z otoczenia poprzez przewodzenie., Po drugie, ciepło jest używane do odparowania płatków, a tym samym ich chłodzenia. Jeśli ciepło parowania „zlewa się” jest większe niż przewodzenie ciepła, płatki pozostaną zamrożone.
okazuje się, że można to łatwo obliczyć. Nie, Nie jest proste obliczenie przewodzenia ciepła lub ciepła parowania, ale stosunek jest, ponieważ różne nieznane czynniki geometryczne anulować.
Jeśli nie zależy ci na obliczeniach (bo nie jesteś maniakiem nauki), możesz po prostu odwiedzić stronę kalkulatora.
Jeśli Ci zależy, to tutaj jest wyprowadzenie., Przypuśćmy, że przepływ wokół płatków jest taki, że wokół niego tworzy się warstwa graniczna o szerokości D. Całkowity przepływ ciepła $F_H$ do płatka (np. J/s W MKS) będzie podany przez prawo Fouriera:
gdzie $\kappa$ jest współczynnikiem dyfuzji ciepła powietrza (np. m2/s W MKS), c jest pojemnością cieplną powietrza (J/kg w MKS), a jest powierzchnią granicy warstwa wokół płatka, podczas gdy δt to różnica temperatur między płatkiem a otoczeniem.,
Podobnie można użyć prawa Ficka, aby uzyskać dyfuzję pary wodnej z płatka (gdzie temperatura jest bliska zamarznięcia, a wilgotność względna wynosi 100%), do otaczającego środowiska, gdzie temperatura jest wyższa, a wilgotność względna niższa:
tutaj D jest współczynnikiem dyfuzji wody (np. m2/s W MKS), a ρ jest gęstością pary wodnej (kg/m3 w MKS).,
parujący lód wymaga ciepła, więc jeśli z płatka wypływa strumień masy pary wodnej Φ, To wymaga ciepła w tempie $F_w = \ epsilon \ Phi$, gdzie $ \ epsilon$ jest ciepłem parowania lodu( J / kg w MKS).
najwyższa temperatura, powyżej której topi się Płatek śniegu, to temperatura, dla której obie przepływy ciepła są sobie równe:
zauważ, że geometria przepływu wokół płatka anuluje się, ponieważ oba strumienie ciepła zależą od d i A w ten sam sposób., Byłoby tak również w przypadku, gdyby warstwa graniczna wokół płatka jest złożona, tak że d rzeczywiście zależy od kierunku. Stąd
gdzie $\rho_ {sat}$ jest nasyconą gęstością pary wodnej.
podstawiając liczby (które można znaleźć np. w podręczniku chemii i fizyki CRC), otrzymujemy Ukryte równanie temperatury, ponieważ nasycenie pary wodnej zależy również od temperatury., Możemy uprościć sprawy, jeśli zamiast tego zapytamy, jaka jest wilgotność względna wymagana do utrzymania płatka zamrożonego w danej temperaturze. Jest to:
gdzie $t_c $ jest temperaturą w stopniu Celsjusza.
tę funkcję można zobaczyć na poniższym rysunku, wraz z danymi z Matsuo i Sasyo, 1981. Jak widać na rysunku, obliczony wykres jest mniej więcej dolną granicą, poniżej której nie ma żadnego deszczu. W cieplejszych temperaturach występuje mieszanka., Do około 1°C powyżej linii bez topnienia występuje głównie śnieg, natomiast od około 1°C do 2°C powyżej linii najczęściej pada deszcz, ale możliwy jest śnieg. Zdarzenia te mogą być spowodowane dodatkowymi efektami, takimi jak silne spadki, czas potrzebny na stopienie śniegu itp.
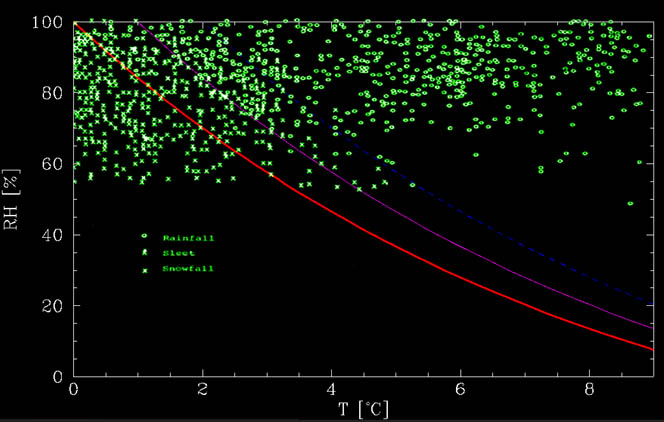
tak więc, jeśli chcemy obserwować Ciepły Śnieg, wymagane są bardzo suche warunki. Na przykład, jeśli wilgotność gruntu wynosi tylko około 20% (bardzo rzadko, ponieważ jeśli występują opady, atmosfera jest ogólnie mokra!) wtedy może padać śnieg w temperaturze 8°C (lub 46°F dla użytkowników angielskich).,
innym wymogiem jest to, że nigdzie wzdłuż zejścia powietrze nie przekracza linii bez stopu. Jeśli tak się stanie, Płatek oczywiście stopi się.
Jeśli temperatura wzrośnie powyżej zera, nie ma parametrów, z którymi można określić rodzaj opadów na pewno. Wszystko, co możemy wtedy przewidzieć, to prawdopodobieństwo, że śnieg faktycznie spadnie. Można to zrobić na podstawie wyników Häggmarka i Ivarssona (1997), skorygowanych tylko w celu użycia mrożonej żarówki, a nie temperatury mokrej żarówki.
w dolnej linii jest kalkulator, za pomocą którego można oszacować prawdopodobieństwo śniegu.,