Zacznijmy od prostego przykładu, powiedzmy, że chcemy pomnożyć (2x-3)3. Nie byłoby to zbyt trudne do zrobienia długiej ręki, ale użyjmy dwumianu twierdzenia tak, że gdy napotkasz większe rozszerzenia, takie jak dwumiany podniesione do 4, 5, 6, … moce będziesz wiedział dokładnie, co zrobić.
aby rozpocząć, musisz zidentyfikować dwa terminy ze swojego dwumianu (pozycje x i y naszego wzoru powyżej) i mocy (n), do której rozszerzasz dwumian.,
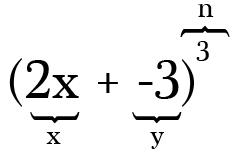
na przykład, aby rozwinąć (2x-3)3, dwa terminy to 2x i -3, a moc, lub wartość n, to 3. Zauważ, że ilekroć masz odejmowanie w dwumianie to jest oh tak ważne, aby pamiętać, aby zawierać minus jako symbol ujemny w towarzyszącym pojęciu.
wspaniałą rzeczą w twierdzeniu dwumianowym jest to, że pozwala nam znaleźć wielomian Rozszerzony bez mnożenia wiązki dwumianów razem. Nieźle, co?, Okazuje się, że liczba pojęć w Twoim wielomianie rozszerzonym będzie zawsze o jeden więcej niż potęga, którą rozszerzasz. Oznacza to, że będziemy tworzyć wielomian z 4 pojęciami, ponieważ moc w tym przykładzie wynosi 3.
każdy termin będzie miał (2x) i (-3), a także wzór „N wybierz k”, gdzie n=3. Możesz to zapisać 4 razy, po jednym dla każdego terminu, pozostawiając wartość k W „N wybierz k” i uprawnienia puste na chwilę.
następnie będziesz chciał wypełnić wartości k i uprawnienia. Tutaj możesz postępować zgodnie ze wzorem sumowania, zwiększając moc dla każdego terminu., Ale dość łatwo jest po prostu podążać za wzorcami.
wartości k W „N wybierz k” rozpoczynają się od k=0 i zwiększają się o 1 w każdym semestrze. Ostatni termin powinien kończyć się n równym k, w tym przypadku n = 3 i k=3.
następnie musimy dodać uprawnienia na (2x) i (-3).
power on (2x) rozpocznie się od wartości n, więc w tym przypadku 3, i zmniejszy się o 1 w każdym termie, dopóki nie osiągniesz zera. Włączanie (-3) rozpocznie się od zera i zwiększy się o jeden za każdym razem, aż dojdziesz do n, lub 3 w tym problemie.,

ponieważ każda wartość podniesiona do potęgi zera jest równa 1, możesz uprościć Warunki za pomocą potęgi zera.

następnie zastosuj uprawnienia i uprość je tam, gdzie to możliwe.,

Skrót trójkąta Pascala

ostatnią częścią jest rozwiązanie formuły kombinacji. Oczywistym sposobem na to jest zastosowanie formuły kombinacji dla każdego problemu. Ale zrobimy tu miły Skrót używając trójkąta Pascala.
trójkąt Pascala jest prostym, ale potężnym trójkątem utworzonym przez utworzenie trójkąta z trzema jedynkami do rozpoczęcia., Dla każdego następnego wiersza po prostu napisz 1 na obu końcach i znajdź środkową liczbę, dodając dwie wartości bezpośrednio nad nią.

teraz jest dobra część. Ukryte w trójkącie Pascala są wszystkie odpowiedzi na dowolne „N wybierz k”! To jak sekretny mały cheatsheet!
poniższy diagram pokazuje, gdzie znajdują się ukryte „N wybierz K”.,

w przypadku naszego problemu musimy rozwiązać: 3 Wybierz 0, 3 Wybierz 1, 3 Wybierz 2 i 3 Wybierz 3. Czyli wszystkie wartości w 4 wierszu. Więc wszystko, co musimy zrobić, to spojrzeć na czwarty rząd trójkąta Pascala i dopasować odpowiedzi.
czwarty wiersz ma wartości: 1, 3, 3, 1. Więc po prostu zamienię odpowiedzi na nasze ” N ” I „k”.,

wreszcie, wszystko, co musisz zrobić, to pomnożyć i uprościć każdy termin do najprostszej formy. Nie zapomnij sprawdzić ostatecznej odpowiedzi, aby upewnić się, że uprawnienia na każdym semestrze nadal dodać do stopnia oryginalnego dwumianu! Zaufaj mi, bardzo łatwo jest popełnić błąd transkrypcji w tego typu problemie 😉
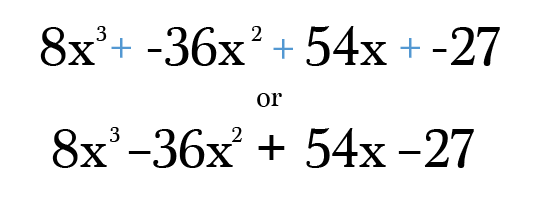
potrzebujesz innego przykładu?,
w powyższym filmiku pokażę Ci, jak wykorzystać twierdzenie dwumianowe do rozszerzenia dwumianu (x – 3y)⁵. Dodatkowo pokażę Ci kilka dodatkowych sztuczek na utrzymanie porządku i kilka szybkich kontroli, których możesz użyć, aby łatwo zidentyfikować typowe błędy.
dzięki za przeczytanie!
STAY bądź w kontakcie❤
Bądź na bieżąco ze wszystkim, co robi Math Hacks!