O “Círculo de Unidade” é um círculo com um raio de 1. sendo tão simples, é uma ótima maneira de aprender e falar sobre comprimentos e ângulos.
O centro é colocado em um grafo onde o eixo x e o eixo y cruzam, então nós obtemos este arranjo limpo aqui.
Seno, co-seno e Tangente
Porque o raio é 1, podemos medir diretamente seno, co-seno e tangente.,
o Que acontece quando o ângulo θ, é de 0°?
cos 0° = 1, sen 0° = 0 e tan de 0° = 0
o Que acontece quando θ é de 90°?
cos 90° = 0, sin 90 ° = 1 e tan 90° é indefinido
Tente você mesmo!
tente!, Mova o mouse ao redor para ver como diferentes ângulos (em radianos ou graus) afetam seno, cosseno e tangente
os “lados” podem ser positivos ou negativos de acordo com as regras das coordenadas cartesianas. Isto faz com que a mudança seno, cosseno e tangente entre valores positivos e negativos também.
tente também o círculo de unidade interactiva.,
Pitágoras
base no Teorema de Pitágoras diz que, para um certo triângulo rectângulo, o quadrado do lado maior igual à soma dos quadrados dos outros dois lados:
x2 + y2 = 12
Mas 12 é apenas 1, assim:
x2 + y2 = 1
(a equação do círculo unitário)
além disso, como x=cos y=pecado, temos:
(cos(θ))2 + (sin(θ))2 = 1
um útil “identidade”
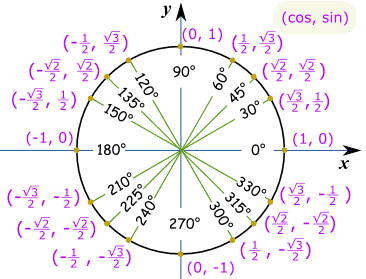
Importante Ângulos de 30°, 45° e 60°
Você deve tentar lembrar-sin, cos e tan para os ângulos de 30°, 45° e 60°.,
Sim, Sim, é uma dor ter que lembrar as coisas, mas vai tornar a vida mais fácil quando você as conhece, não apenas nos exames, mas outras vezes quando você precisa fazer estimativas rápidas, etc.estes são os valores de que se deve lembrar!,id=”0f47f3223b”>
What about tan?,
Bem, tan = sin/cos, de modo que podemos calcular assim:
tan(30°) =sen(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sen(45°)cos(45°) = √2/2√2/2 = 1
tan(60°) =sen(60°)cos(60°) = √3/21/2 = √3
* Nota: texto 1√3 de maio de custo marcas (ver Racional Denominadores), então ao invés de usar √33
Esboço Rápido
Outra maneira de ajudar você a se lembrar de 30° e 60° é fazer um esboço rápido:
| Desenhe um triângulo com lados de comprimentos de 2 | 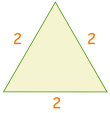 |
|
|
Corte na metade.,div id=”56c966b492″> Exemplo: sen(30°)Seno: sohcahtoa o seno é oposto dividido pela hipotenusa
sin(30°) = oppositehypotenuse = 12
O Círculo InteiroPara todo o círculo precisamos de valores em cada quadrante, com a correta adição ou subtracção, como por Coordenadas Cartesianas: Note que cos é o primeiro e o pecado é a segunda, então ele vai (cos, o pecado):
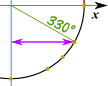
Salvar como PDF Exemplo: o Que é cos(330°) ?,
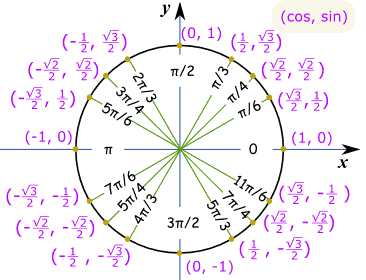
Faça um esboço de como esse, e nós podemos ver que é o “tempo” valor: √32 E este é o mesmo Círculo Unitário em radianos.
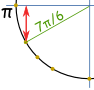
exemplo: o que é o sin(7π / 6) ? Think” 7π/6 = π + π/6″, then make a sketch. Podemos então ver que é negativo e é o valor “Curto”: – ½ |