Content
Constant acceleration
we are all familiar with the fact that a car speeds up when we put our foot down on the accelerator. A velocidade de mudança da velocidade de uma partícula em relação ao tempo é chamada de aceleração. Se a velocidade da partícula muda a uma taxa constante, então esta taxa é chamada de aceleração constante.,
Por exemplo, se a velocidade de uma partícula que se move numa linha recta mudar uniformemente (a uma taxa constante de variação) de 2 m/s para 5 m/s durante um segundo, então a sua aceleração constante é de 3 m/S\(^2\).
redução da velocidade
Se uma partícula tem uma velocidade inicial de 6 m/s e uma aceleração constante de \(-2\) m/s\(^2\), então:
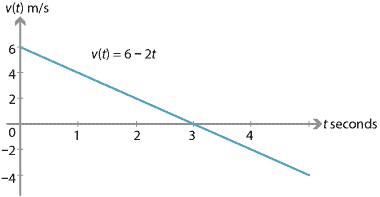
Nos primeiros três segundos, a partícula velocidade está diminuindo (a partícula está a abrandar). Em três segundos, a partícula está momentaneamente em repouso., Após três segundos, a velocidade ainda está diminuindo, mas a velocidade está aumentando (a partícula está indo mais rápido e mais rápido).
Resumo
Se assumir que a taxa de variação da velocidade (aceleração) é uma constante, então a constante aceleração é dada por
\
Mais precisamente, a constante aceleração de \(a\) é dado pela fórmula
\
onde \(v(t_i)\) é a velocidade do tempo \(t_i\). Como a velocidade é um vector, a aceleração também é.,
as fórmulas de aceleração constante para o movimento numa linha recta
ao longo desta secção, temos estado a considerar o movimento numa linha recta com aceleração constante. Esta situação é muito comum; por exemplo, um corpo que se move sob a influência da gravidade viaja com uma aceleração constante.
assume-se que o movimento começa quando \(t = 0\), e que a posição inicial é tomada como a origem, isto é, \(x(0) = 0\).,
Os cinco equações de movimento
- \(v = u + a\)
- \(x = \dfrac{(u+v)t}{2}\)
- \(x = ut + \dfrac{1}{2}a^2\)
- \(v^2 = u^2 + 2ax\)
- \(x = vt – \dfrac{1}{2}a^2\)
Nota. Cada uma das cinco equações envolve quatro das cinco variáveis \(u, v, x, A, t\). Se os valores de três das variáveis são conhecidos, então os valores restantes podem ser encontrados usando duas das equações.,
derivando as fórmulas de aceleração constante
A primeira equação de movimento
desde que a aceleração é constante, temos \(a = \dfrac{v-u}{t}\). Isto dá a primeira equação de movimento, \(v = u + at\).
A segunda equação do movimento
A segunda equação,
\
diz que o deslocamento é obtido multiplicando-se a média inicial e final velocidades pelo tempo decorrido durante o movimento. Mais simplesmente:
\
podemos derivar esta equação usando o fato de que o deslocamento é igual à área assinada sob o grafo velocidade–tempo.,
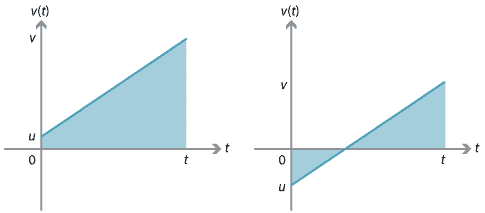
para o grafo à direita, o deslocamento pode ser encontrado considerando os dois triângulos entre o grafo e o eixo \(t\). Um dos triângulos tem uma área assinada positiva e o outro tem uma área assinada negativa.
encontrar o deslocamento de uma partícula a partir do grafo velocidade–tempo usando integração será discutido em uma seção posterior deste módulo.,
A terceira equação do movimento
Substituindo por \(v\) a partir da primeira equação na segunda equação fornece
\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+at)t}{2} \\ &= \dfrac{2ut+a^2}{2} \\ &= ut + \dfrac{1}{2}a^2, \end{align*}
que é a terceira equação. Assim \(x\) é um quadrático em \(t\), e portanto o grafo de \(x\) contra \(t\) é uma parábola.
A quarta equação de movimento
da primeira equação, temos \(t = \dfrac{v-u}{a}\)., Substituindo na segunda equação fornece
\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-u^2}{2a}. \end{align*}
rearranjando para fazer \(v^2\) o sujeito produz a quarta equação: \(v^2 = u^2 + 2ax\).
A quinta equação de movimento
da primeira equação, temos \(u = v-at\)., Usando a segunda equação, obtemos
\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-a+v)t}{2} \\ &= \dfrac{2vt-a^2}{2} \\ &= vt-\dfrac{1}{2}a^2, \end{align*}
o que é a quinta equação.
movimento Vertical
movimento devido à gravidade é um bom contexto no qual demonstrar o uso das fórmulas de aceleração constante., Como discutido anteriormente, nossas duas direções em movimento vertical são para cima e para baixo, e uma decisão tem de ser tomada sobre qual das duas direções é positiva. A aceleração devida à gravidade é uma constante, com magnitude representada por \(g\). No exemplo seguinte, tomamos a direção para cima para ser positivo e tomar \(g = 10\) m/s\(^2\).
Exercício 3
um homem mergulha a partir de um trampolim onde o seu centro de gravidade está inicialmente 12 metros acima da água, e a sua velocidade inicial é 4,9 m/s para cima., Considere o mergulhador como uma partícula em seu centro de gravidade, e assuma que o movimento do mergulhador é vertical.
- Encontre a velocidade do mergulhador após \(t\) segundos (até quando ele atinge a água). Encontre a altura do mergulhador acima da água após \(t\) segundos (até quando ele atinge a água). Encontre a altura máxima do mergulhador acima da água. Encontre o tempo necessário para o mergulhador alcançar a água., Sketch the velocity–time graph for this motion (up to when he hits the water). Sketch the position–time graph for this motion (up to when he hits the water).
além disso, o uso das equações de movimento
Exercício 7
Um carro acelera de 0 km/h a 100 km/h em 10 segundos, e continua por 40 segundos a 100 km/h. Em seguida, o driver freios fortemente para parar de 38 metros.
- Converter 100 km/h para m / s., Encontre a aceleração constante do carro nos primeiros 10 segundos em m / s\(^2\). encontrar a distância total percorrida pelo carro em metros. encontrar a aceleração para a fase de travagem em m / s\(^2\). quanto tempo demora o carro a parar quando os travões são accionados pela primeira vez? Sketch a velocity–time graph for the motion of the car.,
Next page – Content – Average velocity and average speed
 |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |