
A função delta de Dirac é uma função introduzido em 1930, por P. A. M. Dirac em seu livro seminal sobre a mecânica quântica. Um modelo físico que visualiza uma função delta é uma distribuição de massa finita de massa total m-a integral sobre a distribuição de massa., Quando a distribuição se torna menor e menor, enquanto M é constante, a distribuição de massa encolhe para uma massa de ponto, que por definição tem extensão zero e ainda tem uma integral de valor finito igual à massa total M. no limite de uma massa de ponto, a distribuição se torna uma função delta de Dirac.
Heuristic, the Dirac delta function can be seen as an extension of the Kronecker delta from integral indices (elements of 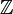 ) to real indices (elements of
) to real indices (elements of 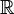 )., Observe que o delta de Kronecker age como um “filtro” em um somatī orio:
)., Observe que o delta de Kronecker age como um “filtro” em um somatī orio:
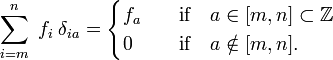
Em analogia, a função delta de Dirac δ(x−a) é definida por (substitua o i por x e a soma sobre i, através de uma integração de x),
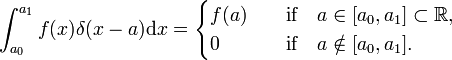
A função delta de Dirac não é um automóvel bem-comportado mapa 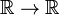 , mas de uma distribuição, também conhecido como inadequado ou generalizada função. Os físicos expressam seu caráter especial afirmando que a função delta de Dirac faz apenas sentido como um fator em uma integranda (“sob a integral”)., Matemáticos dizem que a função delta é uma função linear em um espaço de funções de teste.
, mas de uma distribuição, também conhecido como inadequado ou generalizada função. Os físicos expressam seu caráter especial afirmando que a função delta de Dirac faz apenas sentido como um fator em uma integranda (“sob a integral”)., Matemáticos dizem que a função delta é uma função linear em um espaço de funções de teste.
Conteúdo
- 1 Estabelecimentos
- 2 Delta-convergente sequências
- 2.1 Bloco de funções
- 2.2 Gaussiana funções
- 2.3 Lorentz-Cauchy funções
- 2.4 funções Sinc
- 3 Derivados do delta função
- 3.,1 Propriedades da derivada
- 4 Primitivo
- 5 A função delta de Dirac em três dimensões
- 6 Referências
Propriedades
Mais comumente leva o inferior e o limite superior na definição da função delta igual a 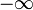 e
e 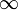 , respectivamente. A partir de agora, isto será feito.
, respectivamente. A partir de agora, isto será feito.
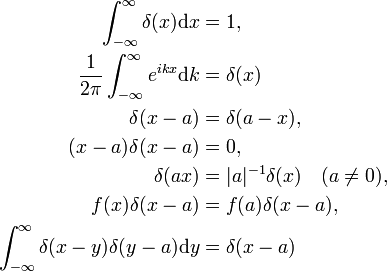
a prova destas propriedades pelo físico procede fazendo substituições adequadas na integral e usando as regras ordinárias do cálculo integral., A função delta como uma transformada de Fourier da função de unidade f (x) = 1 (a segunda propriedade) será provada abaixo. A última propriedade é a analogia da multiplicação de duas matrizes identidade,
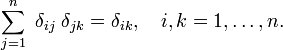
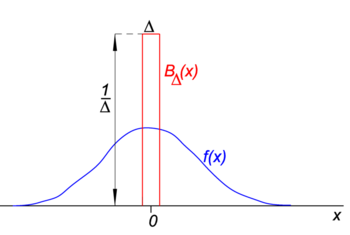
Fig. 1. Bloco (“boxcar”) função (vermelho) vezes função regular f(x) (azul).
sequências Delta-convergentes
existem famílias de Funções Regulares Fa(x) das quais os membros da família diferem pelo valor de um único parâmetro α., Um exemplo de tal família é formado pela família das funções Gaussianas Fa(x) = exp(−ax2), onde os diferentes valores do parâmetro único α distinguem os diferentes membros. Quando todos os membros são linearmente normalizable, por exemplo, a seguinte integral é finito, independentemente de α,
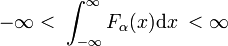
e todos os membros de pico em torno de x = 0, então a família pode formar um delta-sequência convergente.,
funções de bloco
o exemplo mais simples de uma sequência delta-convergente é formado pela família de funções de bloco, caracterizado por Δ positivo,
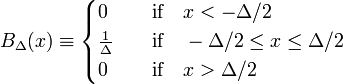
na Fig. 1 a função de bloco BΔ é mostrada em vermelho. Evidentemente, a área (largura vezes altura) sob a curva vermelha é igual a unidade, independentemente do valor de Δ,
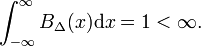
deixe a função arbitrária f(x) (Azul Na Figura. 1) ser contínuo (sem saltos) e finito na vizinhança de x=0., Quando Δ se torna muito pequeno, e a função de bloco muito estreita (e necessariamente muito alta porque largura vezes altura é constante) o produto f(x) BΔ(x) torna-se em boa aproximação igual a f(0) BΔ(x). Quanto mais estreito for o bloco, melhor será a aproximação., Portanto, para Δ vai para zero,
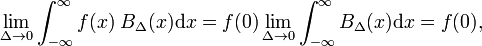
o que pode ser comparado com a definição da função delta,
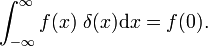
Isso mostra que a família de bloco de funções converge para a função delta de Dirac para a diminuição do parâmetro Δ; a família forma um delta-convergente sequência:
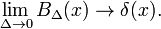
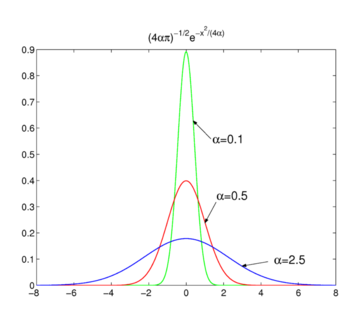
Fig. 2. Funções gaussianas.
Nota: integrámos todo o eixo real., Obviamente isso não é necessário, poderíamos ter excluído as asas de valor zero da função de bloco e integrado apenas sobre o hump no meio, de-Δ / 2 a + Δ / 2. Em textos matemáticos, como por exemplo Ref. , este refinamento nos limites de integração está incluído na definição da sequência delta-convergente. Ou seja, é necessário que as integrais sobre as duas alas desapareçam no limite. Como as sequências delta-convergentes encontradas em aplicações físicas normalmente satisfazem esta condição, omitimos a definição matemática mais exata.,
funções Gaussianas
considere a família,
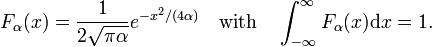
como é mostrado na Fig. 2 as funções atingem o pico em torno de x = 0 e tornam-se mais estreitas para diminuir α. Daí a família de funções Gaussiana forma um delta-convergente seqüência,
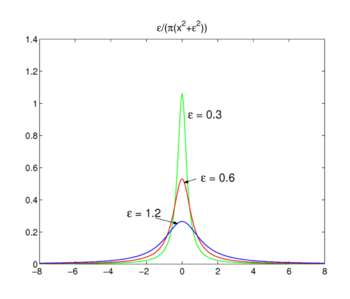
Fig. 3. Lorentz-Cauchy functions
Lorentz-Cauchy functions
The family of functions shown in Fig., 3
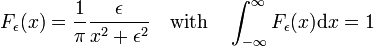
forms a delta-convergent sequence,
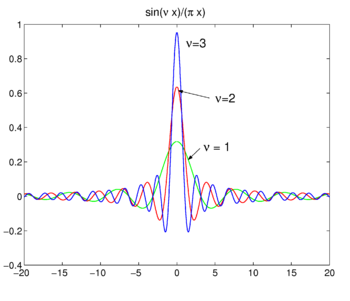
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 é
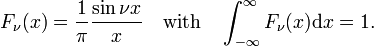
Esta família converge para a função de intervalo para aumentar ν
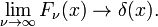
Este limite, leva de imediato ao da integral de Fourier de uma representação da delta de função:
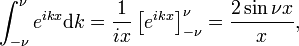
para que
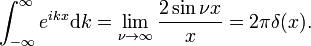
A função delta de Dirac é a transformada de Fourier da unidade função f(x) = 1.
derivados da função delta
considere uma função diferenciável f (x) que desaparece em mais e menos infinito.,d=”ed7dae11d6″>
da mesma forma como uma prova de que o volume de negócios regra e Hermiticity do quantum de impulso mecânico operador 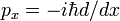 , mostrou-se aqui que d/dx é anti-Hermitiana,
, mostrou-se aqui que d/dx é anti-Hermitiana,
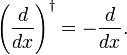
de Fato, quando nós escrever a integral como um produto interno, segue-se a integração parcial e o desaparecimento de f(x) sobre a integração limites
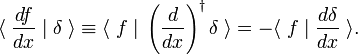
Este volume de negócios regra é usada como a definição da derivada da função delta,
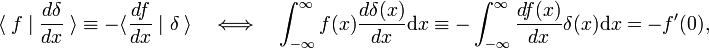
, onde o primeiro indica a primeira derivada de f(x)., De acordo com a definição da função delta, a primeira derivada é avaliada em x = 0. Usando m vezes o volume de negócios de regra, segue-se que o mth derivados do delta função é definida por
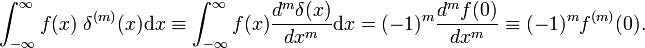
Propriedades do derivado
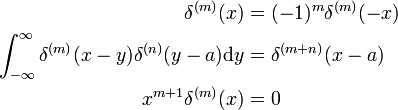
Estes resultados podem ser provados, fazendo a substituição x → −x e a utilização do volume de negócios regra para d/dx (ver acima).,
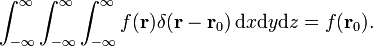
As três dimensões da delta função pode ser factorized
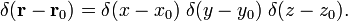
Em coordenadas polares esféricas
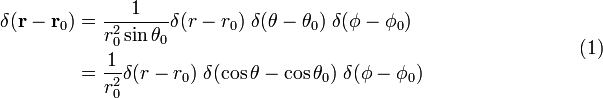
a Prova da equação (1)
Write
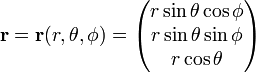
A Razão (Jacobi determinante) esta transformação de coordenadas Cartesianas para coordenadas polares esféricas é
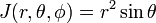
Considere
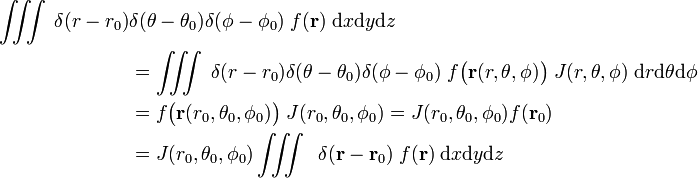
para que
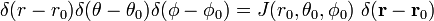
e
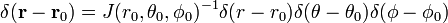
A última linha na equação (1) segue da regra da cadeia.,
O seguinte útil e freqüentemente aplicada propriedade é provado aqui,
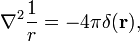
onde ∇2 é o operador de Laplace em três dimensões coordenadas Cartesianas e r é o comprimento do r.