funções logarítmicas são as inversas das funções exponenciais. O inverso da função exponencial y = ax é x = ay. A função logarítmica y = logax é definida como sendo equivalente à equação exponencial x = ay. y = logax apenas sob as seguintes condições: x = ay, a > 0, e a≠1. É chamada de função logarítmica com base A.
considere o que o inverso da função exponencial significa: x = ay., Dado um número x e uma base a, para que poder y deve a ser elevado a igual x? Este expoente desconhecido, y, é igual a logax. Então você vê que um logaritmo não é nada mais do que um expoente. Por definição, alogax = x, para cada real x > 0.
Abaixo são retratados gráficos da forma y = logax quando uma > 1 e 0 < < 1. Observe que o domínio consiste apenas dos números reais positivos, e que a função sempre aumenta à medida que x aumenta.,
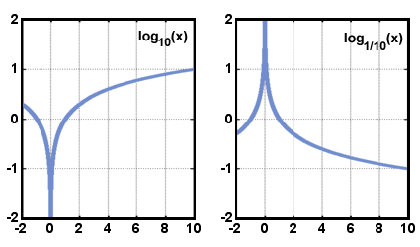
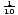 x.
x.O domínio da função logarítmica é números reais maiores do que zero, e o intervalo é de números reais. O grafo de y = logax é simétrico ao grafo de y = ax em relação à linha y = X. Esta relação é verdadeira para qualquer função e seu inverso.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(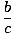 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
Um natural logarítmica função é uma função logarítmica com base e. f (x) = logex = ln x, onde x > 0. ln x é apenas uma nova forma de notação para logaritmos com base E. A maioria das calculadoras tem botões chamados “log” e “ln”. O botão” log “assume que a base é dez, e o botão” ln”, claro, permite que a base seja igual a E., A função logarítmica com base 10 é às vezes chamada de função logarítmica comum. É amplamente utilizado porque o nosso sistema de numeração tem a base dez. Logaritmos naturais são vistos mais frequentemente em cálculo.
Existem duas fórmulas que permitem alterar a base de uma função logarítmica. O primeiro afirma isto: logab = 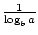 . A fórmula mais famosa e útil para a mudança de bases é comumente chamada de mudança de fórmula de Base. Ele permite que a base de uma função logarítmica seja alterada para qualquer número real positivo ≠1. Indica que logax =
. A fórmula mais famosa e útil para a mudança de bases é comumente chamada de mudança de fórmula de Base. Ele permite que a base de uma função logarítmica seja alterada para qualquer número real positivo ≠1. Indica que logax = 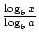 ., Neste caso, a, b e x são todos números reais positivos e a, b≠1.
., Neste caso, a, b e x são todos números reais positivos e a, b≠1.
na próxima seção, discutiremos algumas aplicações de funções exponenciais e logarítmicas.