nestas páginas olhamos para alguns conceitos interessantes, olhamos para o espaço curvado: o que o espaço curvado significa, como podemos dizer se um espaço é curvado de dentro ou de fora dele.
olhamos para como podemos embutir no tipo de espaço dentro de outro e vemos que podemos mapear entre espaços diferentes de maneiras diferentes.
também olhamos para a compacificação e como podemos representar vetores infinitamente grandes e infinitesimalmente pequenos em nossos espaços de maneiras que não levam a singularidades e outros problemas.,
estes conceitos acabam por ser úteis, mesmo quando estamos a trabalhar com espaço plano, vamos encontrar formas de representar vetores e planos que não passam pela origem. Isso nos dá maneiras de representar rotações e traduções como uma única operação.a outra aplicação é o espaço-tempo relativístico.
a geometria de Rienmannian
no espaço de geometria de Rienmannian pode curvar-se em diferentes locais (Ver colectores).,
Eulidean Geometria
espaço plano
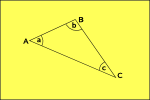
Geometria Hiperbólica
espaço curvas para fora
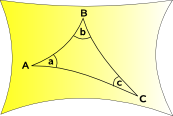
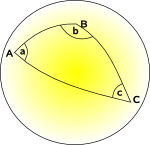
Esférica de Geometria e Geometria Elíptica
espaço curvas para dentro
Em uma curva (Não-Euclidiana) geometria podemos encontrar um conjunto de coordenadas que são mutuamente perpendiculares, onde as linhas de coordenadas são todas paralelas entre si e onde cada quadrado da grade tem a mesma área., Talvez encontremos um sistema de coordenadas onde possamos fazer algumas destas coisas, mas não todas.
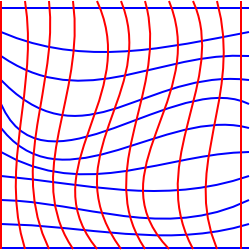
Este diagrama tenta ilustrar esta situação, em 2 dimensões, apesar de ser um pouco enganoso, porque temos desenhado em um plano de modo que poderíamos ter desenhado coordenadas retangulares.para tentar ilustrar uma situação em que isso é impossível, poderíamos pensar num plano bidimensional que foi esticado na terceira dimensão.,

nesta situação podemos escolher coordenadas que formam uma grade retangular quando projetada sobre um plano horizontal, no entanto, para uma pessoa que vive na superfície, em seguida, alguns dos quadrados irá parecem ter uma área maior do que os outros e as linhas de grade podem não parecem ser paralelas. Não existe um sistema de coordenadas bidimensionais que preserve ao mesmo tempo linhas, ângulos e áreas paralelas.,um exemplo similar é tentar mapear a superfície da terra, podemos usar linhas de latitude e longitude, mas as linhas de longitude se aproximam dos pólos.
nestes casos, poderíamos trabalhar em termos de coordenadas tridimensionais e essa é uma abordagem que iremos adoptar com alguns tipos de geometrias não-euclidianas. É muitas vezes possível incorporar uma geometria particular em uma Geometria dimensional mais elevada, a fim de torná-la mais Euclidiana.,
é às vezes o caso de, quando olhamos para uma geometria em grande escala que ela não é Euclidiana, mas se olharmos para ela em uma escala menor e menor então ela se aproxima de uma geometria euclidiana. Para fazer isso, precisamos encontrar um sistema de coordenadas onde os ângulos são preservados em cada ponto, ou seja, as linhas de coordenadas horizontais e verticais precisam sempre Intersectar a 90°, mesmo que as linhas não possam ser retas. Isto é conhecido como uma geometria conforme. Neste tipo de geometria podemos ao menos definir um sistema de coordenadas local.,
relacionado a isso é se a geometria pode ser diferenciada e integrada, uma condição para isso é que ela deve ser bem comportada e não ter quaisquer saltos súbitos, etc. Algumas geometrias e sistemas de coordenadas podem ser bem comportados em alguns lugares, mas têm singularidades, etc.
para discussão sobre como a curvatura é medida veja esta página.
notação matemática
como lidamos com geometrias onde não podemos usar todas as regras que se aplicam à geometria euclidiana?,
uma abordagem é usar Notação tensorial, isto fornece convenções e notação que nos ajudam a mudar entre diferentes sistemas de coordenadas. Um sistema de coordenadas ortogonais, local a qualquer ponto, pode ser definido usando vetores de base que são tangentes às linhas de coordenadas.,Distribuidor
veja esta página.
Relação entre Hiperbólica e Geometria de Minkowski
| Geometria de Minkowski | Geometria Hiperbólica | |
| ponto | evento no espaço-tempo | partícula em movimento uniforme |
| distância entre dois pontos | espaço-intervalo de tempo entre dois eventos | velocidade relativa entre essas duas partículas |
Terminologia
Aqui, vemos a terminologia como geometrias, espaços, modelos, projeções e transformações., É bastante difícil quando começamos a lidar com geometrias não euclidianas porque usamos terminologia semelhante a que estamos acostumados no espaço euclidiano convencional, mas os termos podem ter propriedades ligeiramente diferentes.,tente
Elliptic Geometry
Modelos
Exemplos são:
- metade Superior-modelo de avião
- Poincare modelo de disco
- modelo Projectivo
- Isolante modelo
Projeções
Projeção Estereográfica
Transforma
Invariantes
Exemplos são:
- Transformação de Möbius
- Transformação de Lorentz
Paralelo Postulado
Se a gente tirar o paralelo postulado do Espaço Euclidiano.,
Isto leva a:
- paralelo postulado é false
- os ângulos de um triângulo não adicionar a π
- para uma forma de um determinado tamanho, não em geral, existe uma forma semelhante de um tamanho maior.,ctive
conformal (disco de Poincaré ) linhas retas – geodésia segmentos de círculos ângulo preservar mais os ângulos internos do triângulo π-(α+β+γ)=CΔ distância entre dois pontos com