autómatos Finitos podem ter saídas correspondentes a cada transição. Existem dois tipos de máquinas de estados finitos que geram saída –
- Mealy Máquina
- Moore máquina
Mealy Máquina
uma Mealy máquina é um FSM cuja saída depende do estado atual, bem como da entrada atual.,
pode ser descrito por uma 6 tupla (Q, ∑, O, δ, X, q0) em que −
-
Q é um conjunto finito de Estados.
-
∑ é um conjunto finito de símbolos chamado de alfabeto de entrada.
-
O é um conjunto finito de símbolos chamado de alfabeto de saída.
-
δ é a função de transição de entrada em que δ: Q × ∑ → Q
-
X é a função de transição de saída em que X: Q × ∑ → O
-
q0 é o estado inicial a partir do qual qualquer entrada é processada (q0 ∈ Q).,b424468″>
Output
The state diagram of the above Mealy Machine is −
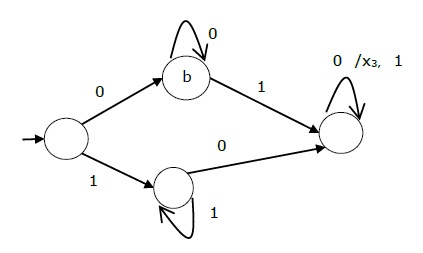
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.,
Uma máquina de Moore pode ser descrita por uma 6 tupla (Q, ∑, O, δ, X, q0) onde −
-
Q é um conjunto finito de Estados.
-
∑ é um conjunto finito de símbolos chamado de alfabeto de entrada.
-
O é um conjunto finito de símbolos chamado de alfabeto de saída.
-
δ é a função de transição de entrada em que δ: Q × ∑ → Q
-
X é a função de transição de saída em que X: Q → O
-
q0 é o estado inicial a partir do qual qualquer entrada é processada (q0 ∈ Q).,iv>
Present state Next State Output Input = 0 Input = 1 → a b c x2 b b d x1 c c d x2 d d d x3 The state diagram of the above Moore Machine is −
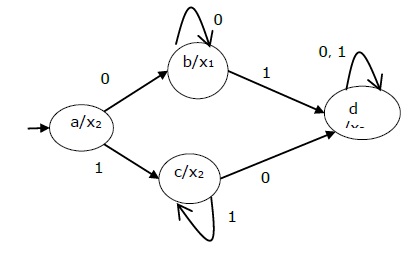
Mealy Machine vs., Moore Machine
a tabela seguinte destaca os pontos que diferenciam uma máquina de Mealy de uma máquina de Moore.
Máquina de Mealy Máquina de Moore Saída depende tanto de um estado presente e o presente de entrada Saída vai depender apenas do estado atual. geralmente, tem menos estados do que Moore Machine. geralmente, tem mais estados do que a máquina Mealy., o valor da função de saída é uma função das transições e das mudanças, quando a lógica de entrada no estado presente é feita. o valor da função de saída é uma função do estado atual e as mudanças nas bordas do relógio, sempre que ocorrem mudanças de Estado. as máquinas de Mealy reagem mais rapidamente às entradas. Eles geralmente reagem no mesmo ciclo de relógio. em máquinas de Moore, mais lógica é necessária para decodificar as saídas resultando em mais atrasos de circuito. Eles geralmente reagem um ciclo de clock mais tarde., Moore Machine to Mealy Machine
algoritmo 4
Input − Moore Machine
Output − Mealy Machine
Step 1 − Take a blank Mealy Machine transition table format.
Passo 2-copiar todos os estados de transição da máquina Moore para este formato de tabela.
Passo 3-Verifique os Estados presentes e suas saídas correspondentes na tabela de Estado da Máquina de Moore; se para um estado Qi saída é m, Copie-o para as colunas de saída da tabela de estado da Máquina de Mealy onde Qi aparece no próximo estado.,der the following Moore machine −
Present State Next State Output a = 0 a = 1 → a d b 1 b a d 0 c c c 0 d b a 1 Now we apply Algorithm 4 to convert it to Mealy Machine.,8″>
Output
Mealy Machine to Moore Machine
Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.,
Passo 2-Se todas as saídas de Qi são iguais, copiar o estado Qi. Se ele tem n Saídas distintas, quebre Qi em n estados como Qin onde n = 0, 1, 2…….
Passo 3 – se a saída do estado inicial for 1, insira um novo estado inicial no início que dê 0 saída.,b424468″>
Output
Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’., Mas os Estados ” b ” E ” c ” produzem resultados diferentes (1 e 0). Então, dividimos b em b0, b1 E c em c0, c1.,”>
Output