vamos começar com um exemplo simples, digamos que queremos multiplicar (2x-3)3. Isso não seria muito difícil de fazer mão longa, mas vamos usar o teorema binomial para que quando você encontrar expansões maiores, como binomiais elevados para os 4, 5, 6, … poderes você saberá exatamente o que fazer.
para começar, você precisa identificar os dois termos do seu binomial (as posições x e y da nossa fórmula acima) e a potência (n) para a qual você está expandindo o binomial.,
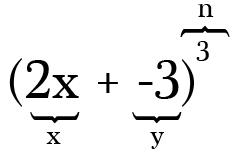
Por exemplo, para expandir (2x-3)3, os dois termos são 2x e -3 e o poder, ou o valor de n, é de 3. Note que sempre que você tem uma subtração em seu binomial é oh tão importante lembrar-se de incluir o menos como um símbolo negativo no termo que acompanha.
a coisa maravilhosa sobre o teorema binomial é que ele nos permite encontrar o polinômio expandido sem multiplicar um monte de binômios juntos. Muito fixe, não é?, Acontece que o número de termos em seu polinômio expandido sempre será um a mais do que o poder que você está expandindo. Isso significa que vamos criar um polinômio com 4 termos, uma vez que o poder neste exemplo é 3.
cada termo terá um (2x) e (-3), bem como a fórmula “N escolher k” onde n=3. Você pode ir em frente e anotar isso 4 vezes, um para cada termo, deixando o valor k em “n Escolha k” e os poderes em branco para o momento.
em seguida, você vai querer preencher os k-valores e poderes. Aqui você pode seguir a fórmula de soma, aumentando o poder para cada termo., Mas é muito fácil apenas seguir os padrões.
os valores de k em “n escolher k”, começarão por k=0 e aumentarão 1 em cada termo. O último termo deve terminar com n igual a k, neste caso n = 3 e k=3.em seguida, precisamos adicionar os poderes em (2x) e (-3).
a potência on (2x) começará com o valor n, então neste caso 3, e diminuirá por 1 em cada termo, até chegar a zero. A energia on (-3) vai começar com zero e aumentar um de cada vez até chegar a n, ou 3 neste problema.,

Devido qualquer valor elevado à potência zero é igual a 1, você pode simplificar os termos com poderes de zero.

em seguida, vá em frente e aplicar os poderes e simplifique sempre que possível.,

O Triângulo de Pascal Atalho

A última parte é para resolver as combinações de fórmula. A forma óbvia de fazer isso é aplicar a fórmula de combinações para cada problema. Mas vamos tomar um pequeno atalho usando o triângulo do Pascal.o triângulo de
Pascal é um triângulo simples, mas poderoso formado pela criação de um triângulo com três 1 para começar., Para cada linha depois, você simplesmente escreve 1’s em ambos os extremos, e encontrar o número do Meio(s), adicionando os dois valores diretamente acima dele.

Agora aqui é a parte boa. Escondidas dentro do triângulo de Pascal estão todas as respostas para qualquer “n Escolha k”! É como um pedaço de carne secreta!
O diagrama abaixo mostra-lhe onde estão localizados os “n escolher K” escondidos.,

Para o nosso problema precisamos resolver para: 3 escolha 0, 3 escolher 1, 3 2, e 3 escolher 3. Que são todos os valores da 4ª linha. Então tudo o que precisamos fazer é olhar para a 4ª fila do triângulo de Pascal e combinar as respostas.
a 4ª linha tem os valores: 1, 3, 3, 1. Por isso, substituo nas respostas os nossos n choose k’s.,

finalmente, tudo o que você precisa fazer é multiplicar e simplificar cada termo até a sua forma mais simples. Não se esqueça de verificar a sua resposta final para se certificar de que os poderes em cada termo ainda adicionar ao grau do seu binomial original! Confie em mim, ele é incrivelmente fácil de fazer uma transcrição de erro neste tipo de problema 😉
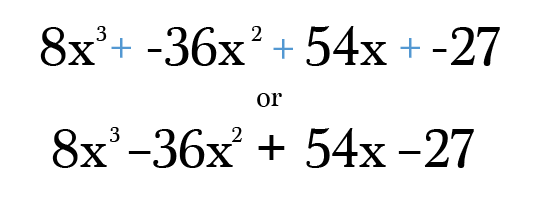
Precisa de outro exemplo?,
no vídeo acima, eu mostro – lhe como usar o teorema Binomial para expandir o binomial (x-3y)⁵. Além disso, eu mostrar – lhe alguns truques adicionais para ficar organizado e um par de verificações rápidas que você pode usar para facilmente identificar erros comuns.obrigado pela leitura!
STAY mantenha-se ligado STAY
Mantenha-se atualizado com tudo o que os Hacks matemáticos estão a fazer!