Encontrar Todas as Raízes de um Polinômio de Função
Use vpasolve para encontrar todas as soluções para a função f(x)=6×7-2×6+3×3-8.
syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)
vpasolve retorna sete raízes da função, conforme o esperado, porque a função é um polinômio de grau sete.,um gráfico da função f (x) = e(x/7) cos (2x) revela zeros periódicos, com o aumento das inclinações nos pontos zero à medida que x aumenta.
syms xh = fplot(exp(x/7)*cos(2*x),);grid on
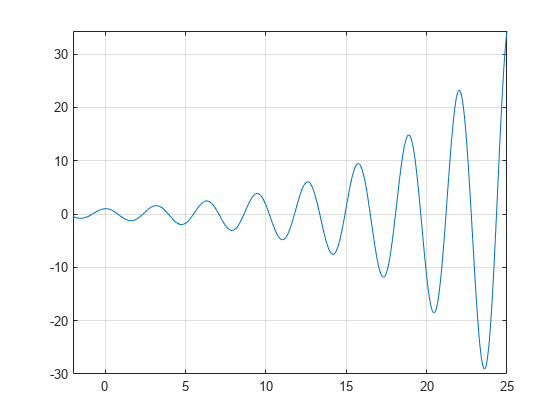
Use vpasolve para encontrar um zero da função f. Note que vpasolve devolve apenas uma solução de uma equação não-polinomial, mesmo que existam várias soluções., On repeated calls, vpasolve returns the same result.
f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.
for k = 1:3 vpasolve(f,x,'Random',true)end
ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')
ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')
ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')
To find a zero close to x=10, set the starting point to 10.,
vpasolve(f,x,10)
ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')
Para encontrar o zero perto de x=1000, definir o ponto de partida para 1000.
vpasolve(f,x,1000)
ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')
Para encontrar o zero no intervalo de 15≤x≤25, defina o intervalo de pesquisa de .,
vpasolve(f,x,)
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
Para encontrar vários zeros no intervalo você não pode chamar vpasolve repetidamente porque ele retorna o mesmo resultado em cada chamada, como mostrado anteriormente. Em vez disso, definir o intervalo de busca e definir 'Random'para true.,
for k = 1:3 vpasolve(f,x,,'Random',true)end
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')
Porque 'Random' seleciona pontos de partida aleatoriamente, a mesma solução pode ser encontrada em chamadas sucessivas.,
Encontre todos os Zeros num intervalo de pesquisa especificado
crie uma função findzerospara encontrar sistematicamente todos os zeros para f numa dada gama de pesquisa, dentro de uma tolerância de erro especificada. A função começa com o intervalo de busca de entrada e chama vpasolve para encontrar um zero. Então, ele divide o intervalo de busca em dois em torno do valor zero e recursivamente se chama com os novos intervalos de busca como entradas para encontrar mais zeros.
A função é explicada seção por seção aqui.,
Declare a função com as três entradas e uma saída. A primeira entrada é a função, a segunda entrada é o intervalo, e a terceira entrada opcional permite que você especifique o erro entre um zero e os limites superior e inferior gerados a partir dele.
function sol = findzeros(f,range,err)
Se você não especificar um argumento opcional para tolerância a erros, findzeros define err 0.001.
if nargin < 2 err = 1e-3;end
Find a zero in the search range using vpasolve.,
sol = vpasolve(f,range);
Se vpasolve não encontrar um zero, sair.
if(isempty(sol)) return
Se vpasolve acha um zero, dividir o intervalo de pesquisa em duas procurar faixas acima e abaixo do zero.
else lowLimit = sol-err; highLimit = sol+err;
Call findzeros com o intervalo de pesquisa mais baixo. Se findzeros devolve zeros, copie os valores para a lista de soluções e separe-os.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end
Call findzeros com o intervalo de pesquisa mais elevado., Se findzeros devolve zeros, copie os valores para a lista de soluções e separe-os.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend
A função inteira findzeros é como se segue. Gravar esta função como findzeros.m na pasta actual.
syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'
Obter Soluções para Precisão Arbitrária
Use digits para definir a precisão das soluções retornadas por vpasolve., Por padrão, vpasolve devolve soluções com uma precisão de 32 figuras significativas.
f = exp(x/7)*cos(2*x);vpasolve(f)
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
Use digits para aumentar a precisão para 64 algarismos significativos. Ao modificar digits, certifique-se de que guarda o seu valor actual para que possa restaurá-lo.,
digitsOld = digits;digits(64)vpasolve(f)
ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')
em seguida, alterar a precisão das soluções para 16 algarismos significativos.
digits(16)
Resolver Equações Multivariadas Utilizando os Intervalos de Pesquisa
Considere o seguinte sistema de equações.
z=10(cos(x)+cos(y))z=x+y2-0.1x2yx+y-2.7=0
Um gráfico de equações para 0≤x≤2,5 e 0≤x≤2.5 mostra que as três faces se interceptam em dois pontos., Para melhor visualizar o gráfico, use view. Para escalar os valores do colormap, use caxis.
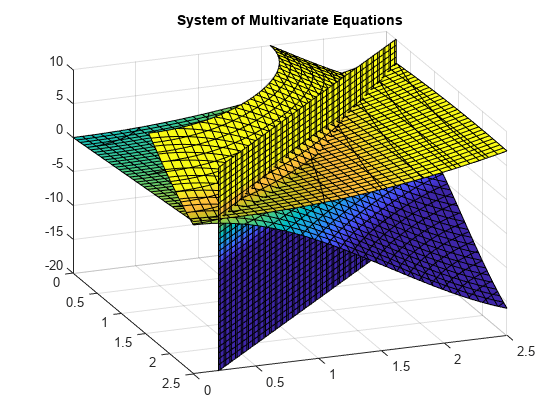
Use vpasolve para encontrar um ponto em que as superfícies se cruzam. A função vpasolve devolve uma estrutura. Para acessar o x-, y e zvalores da solução, o índice para a estrutura.,
sol = vpasolve(equations);
Para pesquisar uma região do espaço de solução, especifique os intervalos de pesquisa para as variáveis. Se indicar os intervalos 0≤x≤1, 5 e 1, 5≤y≤2, 5, então vpasolve a função procura a área delimitada mostrada.

Use vpasolve para encontrar uma solução para este intervalo de pesquisa. Para omitir um intervalo de busca para z, defina o terceiro intervalo de busca para .,
vars = ;range = ;sol = vpasolve(equations, vars, range);
Para encontrar múltiplas soluções, definir o 'Random' opção true. Isto faz com que vpasolve use pontos de partida aleatórios em corridas sucessivas. A opção'Random' pode ser usada em conjunto com intervalos de pesquisa para fazervpasolve usar pontos de partida aleatórios dentro de um intervalo de pesquisa. Porque 'Random' seleciona pontos de partida aleatoriamente, a mesma solução pode ser encontrada em chamadas sucessivas., Ligue para vpasolve repetidamente para garantir que você encontra ambas as soluções.
plotar as equações. Sobrepor as soluções como uma parcela de dispersão de pontos com ID amarelo
marcadores utilizandoscatter3. Para melhor visualizar o enredo, faça duas das superfícies transparentes usando alpha. Dimensionar o colormap para os valores da parcela usando caxis, e alterar a perspectiva usando view.
vpasolve encontra soluções na intersecção das superfícies formadas pelas equações como mostrado.,

Lastly, restore the old value of digits for further calculations.
digits(digitsOld)