secções transversais

propriedades das áreas

Centroid

o centroide de uma forma representa o ponto sobre o qual a área da secção está uniformemente distribuída. Se a área é duplamente simétrica sobre dois eixos ortogonais, o centroide encontra-se na intersecção desses eixos. Se a área é simétrica em torno de apenas um eixo, então o centroide fica em algum lugar ao longo desse eixo (a outra coordenada terá de ser calculada)., Se a exata localização do centróide não pode ser determinado por inspeção, pode ser calculado por:

dA onde representa a área de um infinitamente pequeno elemento, a é a área total da seção transversal, e x e y são as coordenadas do elemento dA com respeito ao eixo de interesse.,

As localizações centroidais das seções transversais comuns estão bem documentadas,por isso normalmente não é necessário calcular a localização com as equações acima., de formas básicas, cuja centroidal locais são conhecidos com relação a algum ponto de referência e, em seguida, o centroidal localização do composto de seção transversal pode ser calculado como:

onde xc e yc,i são as coordenadas retangulares do centroidal localização da i-ésima seção com relação ao ponto de referência, e Ai é a área da i-ésima seção.,

distância Centroidal

a distância centroidal, c, é a distância entre o centroide de uma secção transversal e a fibra extrema., O centroidal distância na direção y para uma seção transversal retangular é mostrado na figura abaixo:

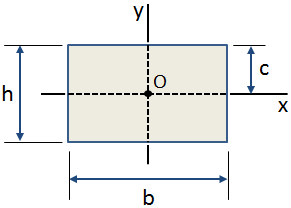
usos Comuns para centroidal distância incluem:

• calcular a máxima tensão de flexão em uma seção transversal
• calcular o valor do primeiro momento de área, Q, acima de um ponto da seção transversal para determinar o “shear stress” em que ponto

Primeiro Momento da Área

O primeiro momento de uma área em relação a um eixo de juros é calculado como:

Qx = ∫ y dA

Qy = ∫ x dA

onde Qx é o primeiro momento sobre o eixo-x e Qy é o primeiro momento sobre o eixo-y.,Se a área é composta por uma coleção de formas básicas, cuja centroidal locais são conhecidos com respeito ao eixo de interesse, em seguida, o primeiro momento do compósito de área pode ser calculado como:

Note que o primeiro momento de a área é usada ao calcular o centróide da seção transversal em relação a alguns origem (como discutido anteriormente)., O primeiro momento também é usado para calcular o valor do esforço transverso em um determinado ponto da seção transversal. Neste caso, o primeiro momento é calculado para uma área que compõe uma parcela menor da seção transversal, onde a área é delimitada pelos pontos de interesse e fibra extrema (superior ou inferior) da seção transversal. O primeiro momento é calculado sobre um eixo que passa através do eixo da seção transversal.,

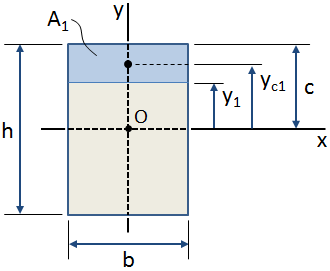
na figura acima, a área azul sombreada é a área de interesse dentro da secção transversal global.,nt da área com relação ao eixo x (que passa através do centróide da seção transversal, ponto S na figura acima) é calculado como:

Se o centroidal localização da área de interesse é conhecida, em seguida, o primeiro momento da área com relação ao eixo pode ser calculado como (veja a figura acima):

deve ser destacado que o primeiro momento de uma área que vai ser positivo ou negativo, dependendo da posição da posição da área em relação ao eixo de interesse., Portanto, o primeiro momento de toda a área de uma seção transversal em relação ao seu próprio centroide será zero.

momento de inércia da área

o segundo momento de área, mais comumente conhecido como o momento de inércia, I, de uma seção transversal é uma indicação da capacidade de um membro estrutural de resistir à flexão.,(Nota 1) Ix e Iy são os momentos de inércia sobre o x – e y – eixos, respectivamente, e são calculados por:

Ix = ∫ y2 dA

Iy = ∫ x2 dA

, onde x e y são as coordenadas do elemento dA com respeito ao eixo de interesse.

Mais comumente, os momentos de inércia são calculados em relação ao centroide da seção. Neste caso, eles são referidos como momentos centroidais de inércia e são denotados como Icx para a inércia sobre o eixo x e gelo para a inércia sobre o eixo y.,

os momentos de inércia das seções transversais comuns estão bem documentados, por isso normalmente não é necessário calculá-los com as equações acima. As propriedades de várias secções transversais comuns são dadas no final desta página.se uma seção transversal é composta por uma coleção de formas básicas cujos centroides são todos coincidentes, então o momento de inércia da seção composta é simplesmente a soma dos momentos individuais de inércia. Um exemplo disso é um feixe de caixa que consiste em duas seções retangulares, como mostrado abaixo., Neste caso, a seção externa tem “área positiva” e a seção interna tem “área negativa”, de modo que o momento de inércia composto é a subtração do momento de inércia da seção interna da seção externa.

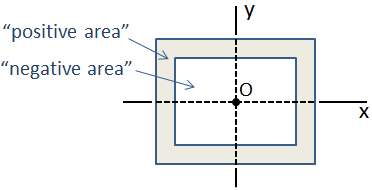
No caso de um problema mais complexo composto de seção transversal na qual o centroidal locais não são coincidentes, o momento de inércia pode ser calculado usando o teorema do eixo paralelo.é importante não confundir o momento de inércia de uma área com o momento de massa de inércia de um corpo sólido., O momento de inércia da área indica a resistência de uma seção transversal à flexão, enquanto o momento de massa de inércia indica a resistência de um corpo à rotação.,

Eixo Paralelo Teorema

Se o momento de inércia da seção transversal sobre um eixo centroidal é conhecido, então o eixo paralelo teorema pode ser usado para calcular o momento de inércia sobre qualquer eixo paralelo:

onde Ic é o momento de inércia sobre o eixo centroidal, d é a distância entre o eixo centroidal e o eixo paralelo, e A é a área da seção transversal.,

Se uma seção transversal é composto por uma coleção de formas básicas, cuja centroidal momentos de inércia são conhecidos juntamente com as distâncias dos centróides para algum ponto de referência e, em seguida, o eixo paralelo teorema pode ser usado para calcular o momento de inércia do compósito de seção transversal.

Por exemplo, um feixe-I pode ser aproximado por 3 retângulos, como mostrado abaixo. Uma vez que esta seção composta é simétrica em relação aos eixos x e y, o eixo da seção pode ser localizado por inspeção na interseção desses eixos. O centroide está localizado na origem, O, na figura.,

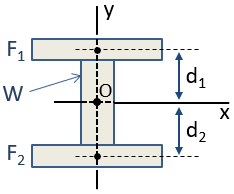
O momento de inércia da composição seção pode ser calculado usando o teorema do eixo paralelo. O momento de inércia centroidal da secção em relação ao eixo dos x, Icx, é calculado como:

onde a Icx termos são os momentos de inércia das seções individuais sobre suas próprias centróides na orientação do eixo-x, os termos d são as distâncias da seção individual de centróides para o composto seção centróide, e em termos são as áreas de cada uma das secções. Como o centroide da seção W e o centroide da seção composta são coincidentes, d é zero para essa seção e então não há nenhum termo Ad2.,

é importante notar a implicação do teorema do eixo paralelo que como uma seção individual se move mais longe do centroide da seção composta, a contribuição dessa seção para o momento de inércia da seção composta aumenta por um fator de d2. Portanto, se a intenção é aumentar o momento de inércia de uma seção sobre um eixo particular, é mais eficiente localizar a área o mais longe possível desse eixo. Isto explica a forma de um I-Beam., As flanges são os principais contribuintes para o momento de inércia, e a web serve para separar as flanges do eixo de flexão. A web não precisa de manter alguma espessura, no entanto, para evitar buckling e porque a web leva uma parte significativa do esforço de cisalhamento na seção.o momento polar de inércia, I, de uma secção transversal é uma indicação da capacidade de um membro estrutural para resistir à torção em torno de um eixo perpendicular à secção., O momento polar de inércia de uma seção com respeito a um eixo pode ser calculado por:

, onde x e y são as coordenadas do elemento dA com respeito ao eixo de interesse, e r é a distância entre o elemento dA e o eixo de interesse.,

Embora o momento polar de inércia pode ser calculado usando a equação acima, é normalmente mais conveniente para calculá-lo usando o eixo perpendicular teorema, que afirma que o momento polar de inércia de uma área é a soma dos momentos de inércia sobre dois eixos ortogonais que passa através do eixo de interesse:

Mais comumente, o eixo de interesse passa através do centróide da seção transversal.,

Módulo de secção

a tensão de flexão máxima num feixe é calculada como σb = Mc / Ic, em que c é a distância do eixo neutro à fibra extrema, Icis o momento centroidal de inércia, e M é o momento de flexão. O módulo de seção combina os Termos c e Ic na equação de tensão de flexão:

Usando o módulo de seção, a tensão de flexão é calculada como σb = M / S. A utilidade do módulo de seção é que ele caracteriza a resistência de flexão de uma seção transversal em um único termo., Isto permite a otimização da seção transversal de um feixe para resistir à flexão maximizando um único parâmetro.

raio de rotação

o raio de rotação representa a distância a partir do centroide de uma secção em que toda a área pode ser concentrada sem ter qualquer efeito no momento de inércia.,>

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration:

Propriedades Comuns Seções transversais

A tabela abaixo apresenta propriedades comuns de seções transversais. As tabelas mais extensas podem ser encontradas nas referências listadas.as propriedades calculadas no quadro incluem a área, o momento centroidal de inércia, o módulo de elasticidade da secção e o raio de rotação.,