Querschnitte

Eigenschaften von Bereichen

Zentroid

Der Schwerpunkt einer Form stellt den Punkt dar, über den die Fläche des Abschnitts gleichmäßig verteilt ist. Wenn der Bereich um zwei orthogonale Achsen doppelt symmetrisch ist, liegt der Schwerpunkt am Schnittpunkt dieser Achsen. Wenn die Fläche nur um eine Achse symmetrisch ist, liegt der Schwerpunkt irgendwo entlang dieser Achse (die andere Koordinate muss berechnet werden)., Wenn der genaue Ort des Schwerpunkts nicht durch Inspektion bestimmt werden kann, kann er berechnet werden durch:

wobei dA die Fläche eines unendlich kleinen Elements darstellt, A die Gesamtfläche des Querschnitts ist und x und y die Koordinaten des Elements dA in Bezug auf die interessierende Achse sind.,

Die zentroidalen Stellen gemeinsamer Querschnitte sind gut dokumentiert, so dass es normalerweise nicht erforderlich ist, die Position mit den obigen Gleichungen zu berechnen., von Grundformen, deren zentroidale Positionen in Bezug auf einen Referenzpunkt bekannt sind,kann die zentroidale Position des zusammengesetzten Querschnitts wie folgt berechnet werden:

wobei xc,i und yc i die rechteckigen Koordinaten der zentroidalen Position des ith-Abschnitts in Bezug auf den Referenzpunkt sind und Ai die Fläche des ith-Abschnitts ist.,

Zentroidalabstand

Der Zentroidalabstand, c, ist der Abstand vom Zentroid eines Querschnitts zur extremen Faser., Der zentroidale Abstand in y-Richtung für einen rechteckigen Querschnitt ist in der folgenden Abbildung dargestellt:

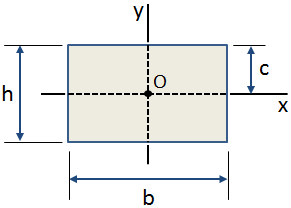
Zu den üblichen Anwendungen für den zentroidalen Abstand gehören:

• Berechnung der maximalen Biegespannung in einem Querschnitt
• Berechnung des Wertes des ersten Flächenmoments Q über einem Punkt im Querschnitt zur Bestimmung der Scherspannung an diesem Punkt

First Moment of Area

Der erste Moment einer Fläche in Bezug auf eine interessierende Achse wird berechnet als:

Qx = ∫ y dA

Qy = ∫ x dA

wobei Qx der erste Moment über die x-Achse und Qy der erste Moment über die y-Achse ist.,Wenn der Bereich aus einer Sammlung von Grundformen besteht, deren zentroidale Positionen in Bezug auf die interessierende Achse bekannt sind, kann der erste Moment des zusammengesetzten Bereichs wie folgt berechnet werden:

Beachten Sie, dass der erste Moment des Bereichs bei der Berechnung des Schwerpunkts eines Querschnitts in Bezug auf einen Ursprung verwendet wird (wie zuvor besprochen)., Das erste Moment wird auch verwendet, wenn der Wert der Scherspannung an einem bestimmten Punkt im Querschnitt berechnet wird. In diesem Fall wird das erste Moment für eine Fläche berechnet, die einen kleineren Teil des Querschnitts ausmacht, wobei die Fläche durch den Punkt von Interesse und die extreme Faser (oben oder unten) des Querschnitts begrenzt wird. Der erste Moment wird um eine Achse berechnet, die durch den Mittelpunkt des Querschnitts verläuft.,

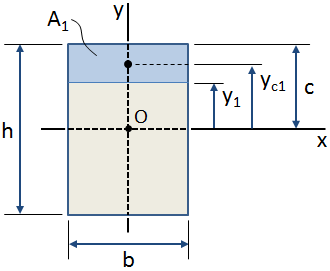
In der obigen Abbildung ist der schattierte blaue Bereich der interessierende Bereich innerhalb des Gesamtquerschnitts.,nt dieses Bereichs in Bezug auf die x-Achse (die den Querschnittszentroid durchläuft, Punkt O in der obigen Abbildung) wird wie folgt berechnet:

Wenn die zentroidale Position des interessierenden Bereichs bekannt ist, kann der erste Moment des Bereichs in Bezug auf die Achse wie folgt berechnet werden (siehe Abbildung oben):

Es ist zu beachten, dass der erste Moment eines Bereichs abhängig von der Position der Position des Bereichs in Bezug auf die interessierende Achse positiv oder negativ ist., Daher ist der erste Moment der gesamten Fläche eines Querschnitts in Bezug auf seinen eigenen Schwerpunkt Null.

Bereich Trägheitsmoment

Das zweite Moment der Fläche, besser bekannt als das Trägheitsmoment I eines Querschnitts, ist ein Hinweis auf die Biegefähigkeit eines Strukturelements.,(Anmerkung 1) Ix und Iy sind die Trägheitsmomente über die x – und y – Achse und werden berechnet durch:

Ix = ∫ y2 dA

Iy = ∫ x2 dA

wobei x und y die Koordinaten des Elements dA in Bezug auf die interessierende Achse sind.

Am häufigsten werden die Trägheitsmomente in Bezug auf den Schwerpunkt des Abschnitts berechnet. In diesem Fall werden sie als zentroidale Trägheitsmomente bezeichnet und als Icx für die Trägheit um die x-Achse und Icy für die Trägheit um die y-Achse bezeichnet.,

Die Trägheitsmomente von gemeinsamen Querschnitten sind gut dokumentiert, so dass es typischerweise nicht notwendig ist, sie mit den obigen Gleichungen zu berechnen. Eigenschaften von mehreren gemeinsamen Querschnitten sind am Ende dieser Seite angegeben.

Wenn ein Querschnitt aus einer Sammlung von Grundformen besteht, deren Zentroide alle zusammenfallen, dann ist das Trägheitsmoment des zusammengesetzten Abschnitts einfach die Summe der einzelnen Trägheitsmomente. Ein Beispiel hierfür ist ein Kastenstrahl, der aus zwei rechteckigen Abschnitten besteht, wie unten gezeigt., In diesem Fall hat der äußere Abschnitt einen “ positiven Bereich „und der innere Abschnitt einen“ negativen Bereich“, so dass das zusammengesetzte Trägheitsmoment die Subtraktion des Trägheitsmoments des inneren Abschnitts vom äußeren Abschnitt ist.

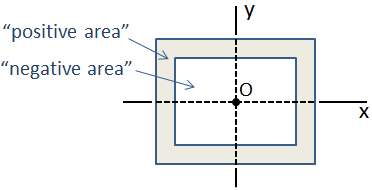
Im Falle eines komplizierteren zusammengesetzten Querschnitts, bei dem die Zentroidalstellen nicht übereinstimmen, kann das Trägheitsmoment mit dem Satz der parallelen Achse berechnet werden.

Es ist wichtig, das Trägheitsmoment eines Bereichs nicht mit dem Massenträgheitsmoment eines festen Körpers zu verwechseln., Das Massenträgheitsmoment zeigt den Biegewiderstand eines Querschnitts an, während das Massenträgheitsmoment den Widerstand eines Körpers gegen Rotation anzeigt.,

Satz der parallelen Achse

Wenn das Trägheitsmoment eines Querschnitts um eine Zentroidalachse bekannt ist, kann der Satz der parallelen Achse verwendet werden, um das Trägheitsmoment um eine parallele Achse zu berechnen:

wobei Ic das Trägheitsmoment um die Zentroidalachse ist, d der Abstand zwischen der Achse und der Achse zentroidalachse und die parallele Achse, und A ist die Fläche des Querschnitts.,

Wenn ein Querschnitt aus einer Sammlung von Grundformen besteht, deren zentroidale Trägheitsmomente zusammen mit den Abständen der Zentroide zu einem Referenzpunkt bekannt sind, kann der Satz der parallelen Achse verwendet werden, um das Trägheitsmoment des zusammengesetzten Querschnitts zu berechnen.

Zum Beispiel kann ein I-Strahl durch 3 Rechtecke angenähert werden, wie unten gezeigt. Da dieser zusammengesetzte Abschnitt sowohl um die x – als auch um die y – Achse symmetrisch ist, kann der Schwerpunkt des Abschnitts durch Inspektion am Schnittpunkt dieser Achsen lokalisiert werden. Der Schwerpunkt befindet sich am Ursprung, O, in der Figur.,

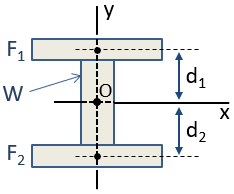
Das Trägheitsmoment des zusammengesetzten Abschnitts kann mithilfe des Satzes der parallelen Achse berechnet werden. Das zentroidale Trägheitsmoment des Abschnitts über die x-Achse, Icx, wird berechnet als:

wobei die Icx-Terme die Trägheitsmomente der einzelnen Abschnitte um ihre eigenen Zentroide in der Ausrichtung der x-Achse sind, sind die d-Terme die Abstände der einzelnen Abschnittszentroide zum zusammengesetzten Abschnittszentroiden und die A-Terme die Bereiche der einzelnen Abschnitte. Da der Schwerpunkt des Abschnitts W und der Schwerpunkt des zusammengesetzten Abschnitts übereinstimmen, ist d für diesen Abschnitt Null und daher gibt es keinen Ad2-Term.,

Es ist wichtig, die Implikation des Satzes der parallelen Achse zu beachten, dass der Beitrag dieses Abschnitts zum Trägheitsmoment des zusammengesetzten Abschnitts um den Faktor d2 zunimmt, wenn sich ein einzelner Abschnitt weiter vom Schwerpunkt des zusammengesetzten Abschnitts entfernt. Wenn daher beabsichtigt wird, das Trägheitsmoment eines Abschnitts um eine bestimmte Achse zu erhöhen, ist es am effizientesten, den Bereich so weit wie möglich von dieser Achse entfernt zu lokalisieren. Dies erklärt die Form eines I-Balkens., Die Flansche tragen hauptsächlich zum Trägheitsmoment bei, und die Bahn dient dazu, die Flansche von der Biegeachse zu trennen. Die Bahn muss jedoch eine gewisse Dicke beibehalten, um ein Knicken zu vermeiden, und da die Bahn einen erheblichen Teil der Scherspannung in dem Abschnitt einnimmt.

Polares Trägheitsmoment

Das polare Trägheitsmoment I eines Querschnitts ist ein Hinweis auf die Fähigkeit eines Strukturelements, der Torsion um eine Achse senkrecht zum Querschnitt zu widerstehen., Das polare Trägheitsmoment für einen Abschnitt in Bezug auf eine Achse kann berechnet werden durch:

wobei x und y die Koordinaten des Elements dA in Bezug auf die interessierende Achse und r der Abstand zwischen dem Element dA und der interessierenden Achse sind.,

Obwohl das polare Trägheitsmoment anhand der obigen Gleichung berechnet werden kann, ist es typischerweise bequemer, es mit dem Satz der senkrechten Achse zu berechnen, der besagt, dass das polare Trägheitsmoment einer Fläche die Summe der Trägheitsmomente über zwei beliebige orthogonale Achsen ist, die durch die interessierende Achse verlaufen:

Am häufigsten passiert die interessierende Achse durch den Schwerpunkt der Fläche.des Querschnitts.,

Schnittmodul

Die maximale Biegespannung in einem Träger wird berechnet als σb = Mc / Ic, wobei c der Abstand von der Neutralachse zur extremen Faser ist, Icis das zentroidale Trägheitsmoment und M das Biegemoment ist. Der Schnittmodul kombiniert die Begriffe c und Ic in der Biegespannungsgleichung:

Unter Verwendung des Schnittmoduls wird die Biegespannung als σb = M / S berechnet., Dies ermöglicht eine Optimierung des Querschnitts eines Balkens, um dem Biegen zu widerstehen, indem ein einzelner Parameter maximiert wird.

Kreiselradius

Der Kreiselradius stellt den Abstand zum Schwerpunkt eines Abschnitts dar, bei dem der gesamte Bereich konzentriert werden kann, ohne den Trägheitsmoment zu beeinflussen.,>

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration: