conținut
accelerație constantă
suntem cu toții familiarizați cu faptul că o mașină accelerează atunci când punem piciorul pe accelerator. Rata de schimbare a vitezei unei particule în raport cu timpul se numește accelerația acesteia. Dacă viteza particulei se schimbă la o rată constantă, atunci această rată se numește accelerație constantă.,de exemplu, dacă viteza unei particule care se deplasează într-o linie dreaptă se schimbă uniform (la o rată constantă de schimbare) de la 2 m/s la 5 m/s pe o secundă, atunci accelerația sa constantă este de 3 m/s\(^2\).dacă o particulă are o viteză inițială de 6 m/s și o accelerație constantă de \(-2\) m/s\(^2\), atunci:
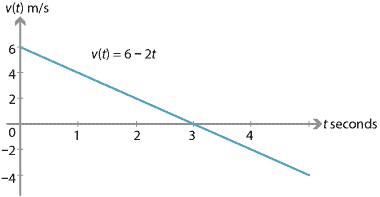
în primele trei secunde, viteza particulei scade (particula încetinește). La trei secunde, particula este momentan în repaus., După trei secunde, viteza este încă în scădere, dar viteza crește (particula merge mai repede și mai repede).
Sumar
Dacă presupunem că rata de schimbare a vitezei (de accelerare) este o constantă, atunci accelerație constantă este dată de
\
Mai exact, accelerație constantă \(o\) este dat de formula
\
unde \(v(t_i)\) este viteza la momentul \(t_i\). Deoarece viteza este un vector, la fel și accelerația.,
formulele de accelerație constantă pentru mișcare în linie dreaptă
pe parcursul acestei secțiuni, am avut în vedere mișcarea în linie dreaptă cu accelerație constantă. Această situație este foarte frecventă; de exemplu, un corp care se mișcă sub influența gravitației călătorește cu o accelerație constantă.se presupune că mișcarea începe când \(t = 0\) și că poziția inițială este luată ca origine, adică \(x(0) = 0\).,
Cele cinci ecuații de mișcare
- \(v = u + at\)
- \(x = \dfrac{(u+v)t}{2}\)
- \(x = ut + \dfrac{1}{2}de la^2\)
- \(v^2 = u^2 + 2ax\)
- \(x = vt – \dfrac{1}{2}de la^2\)
Notă. Fiecare dintre cele cinci ecuații implică patru dintre cele cinci variabile \(u, v, x, a, t\). Dacă valorile a trei dintre variabile sunt cunoscute, atunci valorile rămase pot fi găsite folosind două dintre ecuații.,
derivând formulele de accelerație constantă
prima ecuație de mișcare
deoarece accelerația este constantă, avem \(a = \ dfrac{v-u}{t}\). Aceasta oferă prima ecuație de mișcare, \(v = u + at\).
a doua ecuație de mișcare
a doua ecuație,
\
spune că deplasarea este obținută prin înmulțirea mediei vitezelor inițiale și finale cu timpul scurs în timpul mișcării. Mai simplu:
\
putem deriva această ecuație folosind faptul că deplasarea este egală cu aria semnată sub graficul viteză–timp.,
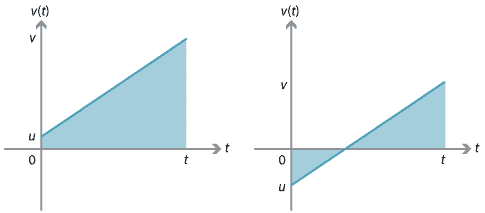
pentru graficul din dreapta, deplasarea poate fi găsită luând în considerare cele două triunghiuri dintre Grafic și axa \(t\). Unul dintre triunghiuri are o zonă semnată pozitivă, iar celălalt are o zonă semnată negativă.găsirea deplasării unei particule din graficul viteză–timp folosind integrarea va fi discutată într-o secțiune ulterioară a acestui modul.,
Cea de-a treia ecuație de mișcare
Substituie \(v\) din prima ecuație în cea de-a doua ecuație oferă
\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+at)t}{2} \\ &= \dfrac{2ut+la^2}{2} \\ &= ut + \dfrac{1}{2}de la^2, \end{align*}
care este cea de-a treia ecuație. Astfel \(x\) este un patratic în \(t\) și, prin urmare, graficul \(x\) împotriva \(t\) este o parabolă.
a patra ecuație de mișcare
Din prima ecuație, avem \(t = \dfrac{v-u}{a}\)., Înlocuind în a doua ecuație oferă
\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-r^2}{2a}. \ end{align*}
rearanjarea pentru a face \(v^2\) subiectul produce a patra ecuație: \(v^2 = u^2 + 2AX\).
a cincea ecuație de mișcare
Din prima ecuație, avem \(u = v-at\)., Folosind cea de-a doua ecuație, obținem
\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-at+v)t}{2} \\ &= \dfrac{2vt-la^2}{2} \\ &= vt-\dfrac{1}{2}de la^2, \end{align*}
care este cea de-a cincea ecuație.
mișcarea verticală
mișcarea datorată gravitației este un context bun în care se demonstrează utilizarea formulelor de accelerație constantă., Așa cum am discutat mai devreme, cele două direcții ale noastre în mișcare verticală sunt în sus și în jos și trebuie luată o decizie cu privire la care dintre cele două direcții este pozitivă. Accelerația datorată gravitației este o constantă, cu magnitudine notată cu \(g\). În exemplul următor, luăm direcția în sus pentru a fi pozitivă și luăm \(g = 10\) m/s\(^2\).
Exercițiul 3
un om se scufundă de pe o rampă de lansare unde centrul său de greutate este inițial la 12 metri deasupra apei, iar viteza sa inițială este de 4,9 m/s în sus., Priviți scafandrul ca o particulă în centrul său de greutate și presupuneți că mișcarea scafandrului este verticală.
- găsiți viteza scafandrului după \(t\) secunde (până când atinge apa).
- găsiți înălțimea scafandrului deasupra apei după \(t\) secunde (până când atinge apa).
- găsiți înălțimea maximă a scafandrului deasupra apei.
- găsiți timpul necesar pentru ca scafandrul să ajungă la apă.,
- schițați graficul viteză–timp pentru această mișcare (până când atinge apa).
- schițați graficul poziție–timp pentru această mișcare (până când atinge apa).
utilizarea ulterioară a ecuațiilor de mișcare
exercițiul 7
o mașină accelerează de la 0 km/h la 100 km/h în 10 secunde și continuă timp de 40 de secunde la 100 km / h. șoferul frânează puternic pentru a opri în 38 de metri.
- convertiți 100 km/h în m / s.,
- găsiți accelerația constantă a mașinii pentru primele 10 secunde în m / s\(^2\).
- găsiți distanța totală parcursă de mașină în metri.
- găsiți accelerația pentru faza de frânare în m / s\(^2\).
- cât timp durează mașina să se oprească la prima aplicare a frânelor?
- schițați un grafic de viteză–timp pentru mișcarea mașinii.,
Next page – Content – Average velocity and average speed
 |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |