
delta Dirac funcție este o funcție a introdus în 1930 de P. A. M. Dirac în seminale carte despre mecanica cuantică. Un model fizic care vizualizează o funcție delta este o distribuție de masă a masei totale finite M-integral peste distribuția de masă., Când distribuția devine din ce în ce mai mică, în timp ce M este constantă, distribuția masei se micșorează la o masă punctuală, care, prin definiție, are o întindere zero și totuși are o integrală finită egală cu masa totală M. În limita unei mase punctuale, distribuția devine o funcție Delta Dirac.
Euristic, în delta Dirac funcție poate fi văzut ca o extensie a delta Kronecker la integrantă indici (elemente de 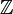 ) pentru real indici (elemente de
) pentru real indici (elemente de 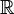 )., Rețineți că delta Kronecker actioneaza ca un „filtru”, într-o însumare:
)., Rețineți că delta Kronecker actioneaza ca un „filtru”, într-o însumare:
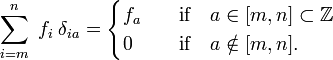
În analogie, delta Dirac funcția δ(x−a) este definit de (înlocuiți am prin x și însumarea peste am de o integrare pe x),
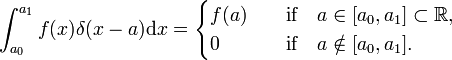
delta Dirac funcția nu este un obișnuit bine-au comportat harta 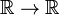 , dar, de distribuție, de asemenea, cunoscut ca un necorespunzătoare sau generalizate funcție. Fizicienii își exprimă caracterul special afirmând că funcția Delta Dirac are sens doar ca factor într-un integrand („sub integral”)., Matematicienii spun că funcția delta este o funcție liniară pe un spațiu de funcții de testare.
, dar, de distribuție, de asemenea, cunoscut ca un necorespunzătoare sau generalizate funcție. Fizicienii își exprimă caracterul special afirmând că funcția Delta Dirac are sens doar ca factor într-un integrand („sub integral”)., Matematicienii spun că funcția delta este o funcție liniară pe un spațiu de funcții de testare.
Cuprins
- 1 Proprietăți
- 2 Delta-convergente secvențe
- 2.1 Bloc de funcții
- 2.2 Gaussian funcții
- 2.3 Lorentz-Cauchy funcțiilor
- 2.4 Sinc funcții
- 3 Derivate din delta funcția
- 3.,1 Proprietățile derivate
- 4 Primitiv
- 5 Dirac delta funcționa în trei dimensiuni
- 6 Bibliografie
Proprietati
cel Mai frecvent ia inferioară și limita superioară în definiția delta funcția egal cu 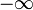 și
și 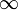 , respectiv. De aici încolo, acest lucru se va face. dovada fizicianului acestor proprietăți se realizează prin înlocuirea corespunzătoare a integralei și prin utilizarea regulilor obișnuite ale calculului integral., Funcția delta ca transformare Fourier a funcției unității f (x) = 1 (a doua proprietate) va fi dovedită mai jos. Ultima proprietate este analogia de înmulțire a două matrice identitate,
, respectiv. De aici încolo, acest lucru se va face. dovada fizicianului acestor proprietăți se realizează prin înlocuirea corespunzătoare a integralei și prin utilizarea regulilor obișnuite ale calculului integral., Funcția delta ca transformare Fourier a funcției unității f (x) = 1 (a doua proprietate) va fi dovedită mai jos. Ultima proprietate este analogia de înmulțire a două matrice identitate,
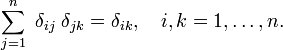
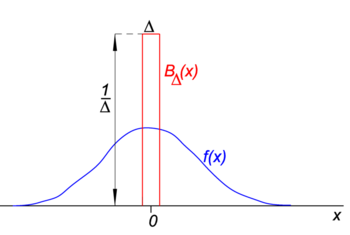
Fig. 1. Block („boxcar”) funcția(Roșu) ori funcția regulată f (x) (albastru).
secvențe convergente Delta
există familii de funcții regulate Fa(x) din care membrii familiei diferă prin valoarea unui singur parametru α., Un exemplu de astfel de familie este format din familia funcțiilor gaussiene Fa(x) = exp(−ax2), unde diferitele valori ale parametrului unic α disting diferiții membri. Atunci când toți membrii sunt liniar normalizable, de exemplu, următoarele integrantă este finit, indiferent de α,
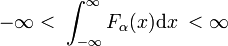
și toți membrii de vârf în jurul valorii x = 0, atunci familia se poate forma un delta-șiruri convergente.,
funcții bloc
cel mai simplu exemplu de secvență delta-convergentă este format din familia funcțiilor bloc, caracterizată prin Δ pozitiv,
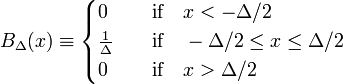
în Fig. 1 Funcția bloc BΔ este afișată în roșu. Evident, aria (lățimea ori înălțimea) de sub curba roșie este egală cu unitatea, indiferent de valoarea Δ,
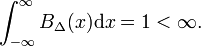
fie funcția arbitrară f(x) (albastru în Fig. 1) să fie continuu (fără salturi) și finit în vecinătatea x=0., Când Δ devine foarte mic, iar funcția bloc foarte îngust (și neapărat foarte mare, deoarece lățimea de ori înălțimea este constantă) produsul f(x) BΔ(x) devine în bună aproximare egal cu f(0) BΔ(x). Cu cât blocul este mai îngust, cu atât aproximarea este mai bună., Prin urmare, pentru Δ merge la zero,
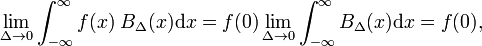
care poate fi comparat cu definiția din delta funcție,
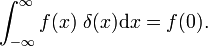
Acest lucru arată că familia de bloc de funcții converge la delta Dirac funcție de scăderea parametrului Δ; familia formează o deltă-șiruri convergente:
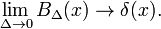
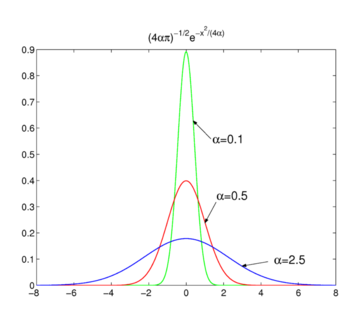
Fig. 2. Funcții gaussiene.
Notă: Am integrat pe întreaga axă reală., Evident, acest lucru nu este necesar, am fi putut exclude aripile cu valoare zero ale funcției blocului și am integrat doar peste cocoașa din mijloc, de la-Δ/2 la +Δ/2. În textele matematice, ca de exemplu Ref. , această rafinare în limitele de integrare este inclusă în definiția secvenței delta-convergente. Adică, este necesar ca integralele peste cele două aripi să dispară în limită. Deoarece secvențele delta-convergente întâlnite în aplicațiile fizice satisfac de obicei această condiție, omitem definiția matematică mai exactă.,
funcții gaussiene
luați în considerare familia,
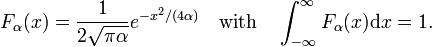
așa cum se arată în Fig. 2 funcțiile ating un vârf în jurul valorii de x = 0 și devin mai înguste pentru scăderea α. Prin urmare, familia de funcții Gaussiene formeaza o delta-șiruri convergente,
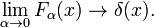
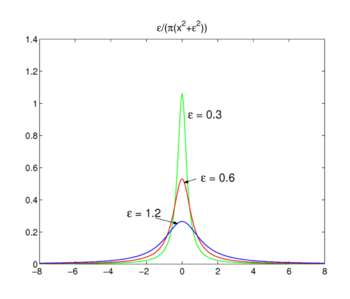
Fig. 3. Funcțiile Lorentz-Cauchy
funcțiile Lorentz-Cauchy
familia de funcții prezentată în Fig., 3
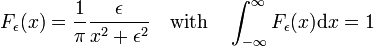
forms a delta-convergent sequence,
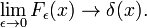
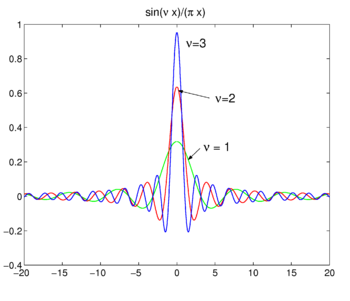
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 este
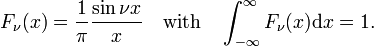
Această familie converge la funcția delta pentru creșterea ν
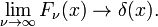
Această limită duce ușor la Fourier reprezentarea integrala a deltei funcția:
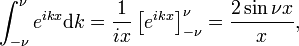
astfel încât
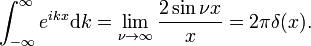
delta Dirac funcție este transformata Fourier a unității funcția f(x) = 1.
derivatele funcției delta
consideră o funcție diferențiabilă f (x) care dispare la infinit plus și minus.,d=”ed7dae11d6″>
În același mod ca o dovedește cifra de afaceri regulă și Hermiticity de mecanică cuantică impuls operator 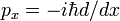 , i-am arătat aici că d/dx este anti-Hermitian,
, i-am arătat aici că d/dx este anti-Hermitian,
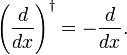
într-Adevăr, când ne-am scrie integral ca produsul scalar, rezultă dintr-o integrare parțială și fuga de f(x) pe de integrare limitele
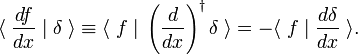
Aceasta cifra de afaceri de regulă este utilizat ca definiție a derivat din delta funcție,
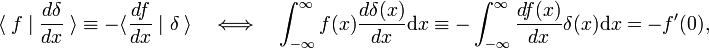
în cazul în care prim-indică prima derivata lui f(x)., Conform definiției funcției delta, primul derivat este evaluat în x = 0. Folosind m ori cifra de afaceri de regulă, rezultă că mth derivate din delta funcția este definită de
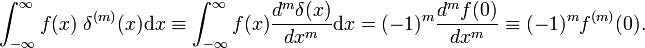
Proprietati derivate
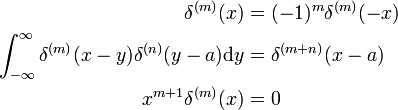
Aceste rezultate poate fi dovedit prin a face substituția x → −x și utilizare a cifrei de afaceri regula pentru d/dx (a se vedea mai sus).,
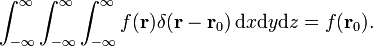
trei-dimensional delta funcție poate fi factorizate
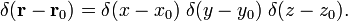
În coordonate polare sferice
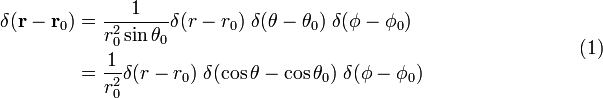
Dovada de ecuația (1)
Scrie
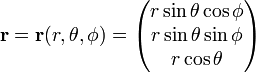
Jacobian (Jacobi determinant) de această transformare de la coordonate Carteziene la coordonate polare sferice este
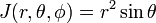
să ne gândim
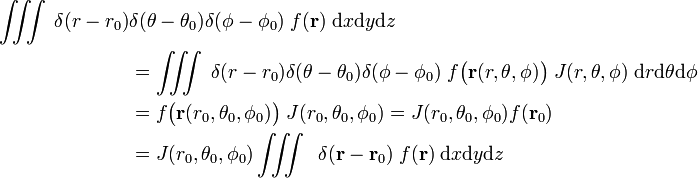
astfel încât
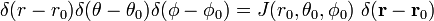
și
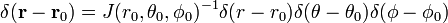
ultima linie în ecuația (1) rezultă din regula lanț.,
următoarele utile și frecvent aplicate de proprietate este dovedit aici,
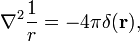
în cazul în care ∇2 este operatorul Laplace în coordonate Carteziene tridimensionale și r este lungimea r.