funcțiile logaritmice sunt inversele funcțiilor exponențiale. Inversul funcției exponențiale y = ax este x = ay. Funcția logaritmică y = logax este definită ca fiind echivalentă cu ecuația exponențială x = ay. y = logax numai în următoarele condiții: x=ay, a > 0 și a≠1. Se numește funcția logaritmică cu baza a.
luați în considerare ce înseamnă inversul funcției exponențiale: x = ay., Având în vedere un număr x și o bază a, la ce putere y trebuie să fie ridicată la x egal? Acest exponent necunoscut, y, este egal cu logax. Deci, vedeți că un logaritm nu este altceva decât un exponent. Prin definiție, alogax = x, pentru fiecare X real > 0.
mai Jos sunt reprezentate graficele de forma y = logax când un > 1 și când 0 < < 1. Observați că domeniul constă numai din numerele reale pozitive și că funcția crește întotdeauna pe măsură ce x crește.,
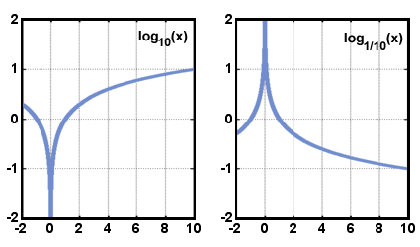
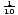 x.
x.domeniu de o funcție logaritmică numere reale este mai mare decât zero, iar gama este numere reale. Graficul lui y = logax este simetric cu graficul lui y = ax în raport cu linia y = x. această relație este adevărată pentru orice funcție și inversul acesteia.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(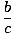 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
Un naturale funcția logaritmică este o funcție logaritmică cu baza e. f (x) = logex = ln x, unde x > 0. ln x este doar o nouă formă de notație pentru logaritmi cu baza e. cele mai multe calculatoare au butoane etichetate „log” și „ln”. Butonul” log „presupune că baza este de zece, iar butonul” ln”, desigur, permite bazei să fie egală cu e., Funcția logaritmică cu baza 10 este uneori numită funcția logaritmică comună. Este utilizat pe scară largă, deoarece sistemul nostru de numerotare are baza zece. Logaritmii naturali sunt văzuți mai des în calcul.există două formule care permit modificarea bazei unei funcții logaritmice. Primul afirmă acest lucru: logab = 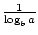 . Formula mai faimoasă și mai utilă pentru schimbarea bazelor este denumită în mod obișnuit schimbarea formulei de bază. Permite schimbarea bazei unei funcții logaritmice la orice număr real pozitiv ≠1. Se afirmă că logax =
. Formula mai faimoasă și mai utilă pentru schimbarea bazelor este denumită în mod obișnuit schimbarea formulei de bază. Permite schimbarea bazei unei funcții logaritmice la orice număr real pozitiv ≠1. Se afirmă că logax = 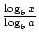 ., În acest caz, a, b și x sunt toate numere reale pozitive și a, b≠1.în secțiunea următoare, vom discuta câteva aplicații ale funcțiilor exponențiale și logaritmice.
., În acest caz, a, b și x sunt toate numere reale pozitive și a, b≠1.în secțiunea următoare, vom discuta câteva aplicații ale funcțiilor exponențiale și logaritmice.