o ipoteză nulă este o afirmație precisă despre o populație pe care încercăm să o respingem cu date de probă.De obicei, nu credem că ipoteza noastră nulă (sau H0) este adevărată. Cu toate acestea, avem nevoie de o declarație exactă ca punct de plecare pentru testarea semnificației statistice.
Exemple de ipoteze nule
adesea-dar nu întotdeauna – ipoteza nulă afirmă că nu există nicio asociere sau diferență între variabile sau subpopulații., Astfel, unele tipice ipotezelor nule sunt:
- corelația între frustrare și agresiune este zero (corelație-analiză);
- venitul mediu pentru bărbați este similară cu cea pentru femei (independent samples t-test);
- Naționalitatea este (perfect) nu au legătură cu muzica preferință (chi-pătrat de independență test);
- media veniturilor populației a fost egale în 2012 printr-2016 (ANOVA cu măsurători repetate).
” Null „nu înseamnă”Zero „
o neînțelegere comună este că” null „implică”zero”. Acest lucru este adesea, dar nu întotdeauna cazul., De exemplu, o ipoteză nulă poate afirma, de asemenea, că corelația dintre frustrare și agresiune este 0.5.No zero implicat aici și – deși oarecum neobișnuit-perfect valabil.
„null” din „ipoteza nulă”derivă din” nullify ” 5: ipoteza nulă este afirmația pe care încercăm să o respingem, indiferent dacă (nu) specifică un efect zero.
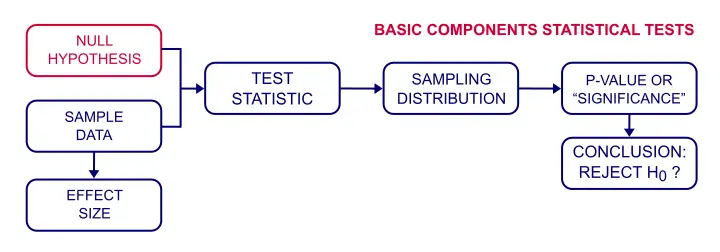
Testarea ipotezelor nule-cum funcționează?
vreau să știu dacă fericirea este legată de bogăție în rândul olandezilor. O abordare pentru a afla acest lucru este de a formula o ipoteză nulă., Deoarece” legat de ” nu este precis, alegem afirmația opusă ca ipoteză nulă: corelația dintre bogăție și fericire este zero între toți olandezii.Vom încerca acum să respingem această ipoteză pentru a demonstra că fericirea și bogăția sunt legate în regulă.
acum, nu putem întreba în mod rezonabil toți cei 17.142.066 de olandezi cât de fericiți se simt în general.

deci, vom cere un eșantion (să zicem, 100 de persoane) despre bogăția și fericirea lor. Corelația dintre fericire și bogăție se dovedește a fi de 0,25 în eșantionul nostru., Acum avem o problemă: rezultatele eșantioanelor tind să difere oarecum de rezultatele populației. Deci, dacă corelația este cu adevărat zero în populația noastră, am putea găsi o corelație non zero în eșantionul nostru. Pentru a ilustra acest punct important, aruncați o privire la scatterplot de mai jos. Vizualizează o corelație zero între fericire și bogăție pentru o întreagă populație de N = 200.

acum tragem un eșantion aleatoriu De N = 20 din această populație (punctele roșii din scatterplot-ul nostru anterior). Chiar dacă corelația noastră de populație este zero, am găsit un uimitor 0.,82 corelație în eșantionul nostru. Figura de mai jos ilustrează acest lucru prin omiterea tuturor unităților neeșantionate din scatterplot-ul nostru anterior.

Acest lucru ridică întrebarea cum putem spune vreodată ceva despre populația noastră dacă avem doar o mică mostră din ea. Răspunsul de bază: rareori putem spune ceva cu 100% certitudine. Cu toate acestea, putem spune multe cu certitudine de 99%, 95% sau 90%.
probabilitate
Deci, cum funcționează asta? Ei bine, practic, unele rezultate eșantion sunt foarte puțin probabil având în vedere ipoteza noastră nulă., Astfel, figura de mai jos arată probabilitățile pentru diferite corelații ale eșantionului (N = 100) dacă corelația populației este cu adevărat zero.

un computer va calcula cu ușurință aceste probabilități. Totuși, acest lucru necesită o dimensiune a eșantionului (100 în cazul nostru) și o corelație presupusă a populației ρ (0 în cazul nostru). De aceea avem nevoie de o ipoteză nulă.
dacă privim cu atenție această distribuție de eșantionare, vedem că corelațiile eșantioanelor în jurul valorii de 0 sunt cele mai probabile: există o probabilitate de 0,68 de a găsi o corelație între -0,1 și 0,1. Ce înseamnă asta?, Ei bine, amintiți-vă că probabilitățile pot fi văzute ca frecvențe relative. Imaginați-vă că am trage 1.000 de mostre în loc de cea pe care o avem. Aceasta ar avea ca rezultat coeficienții de corelație 1,000, iar aproximativ 680 dintre aceștia-o frecvență relativă de 0,68 – ar fi în intervalul -0,1 până la 0,1. De asemenea, există o probabilitate de 0,95 (sau 95%) de a găsi o corelație a eșantionului între -0,2 și 0,2.
valorile P
am găsit o corelație a eșantionului de 0,25. Cât de probabil este că, dacă corelația populației este zero?, Răspunsul este cunoscut sub numele de valoarea p(prescurtarea de la valoarea probabilității): o valoare p este probabilitatea de a găsi un rezultat al eșantionului sau unul mai extrem dacă ipoteza nulă este adevărată.Având în vedere corelația noastră 0.25,” mai extremă ” înseamnă de obicei mai mare decât 0.25 sau mai mică decât -0.25. Nu putem spune din graficul nostru, dar tabelul de bază ne spune că p ≈ 0.012. Dacă ipoteza nulă este adevărată, există o probabilitate de 1,2% de a găsi corelația eșantionului nostru.
concluzie?dacă corelația populației noastre este într-adevăr zero, atunci putem găsi o corelație a eșantionului de 0,25 într-un eșantion de N = 100., Probabilitatea ca acest lucru să se întâmple este de numai 0,012, deci este foarte puțin probabil. O concluzie rezonabilă este că corelația noastră populație nu a fost zero, după toate.
concluzie: respingem ipoteza nulă. Având în vedere rezultatul eșantionului nostru, nu mai credem că fericirea și bogăția nu au legătură. Cu toate acestea, încă nu putem afirma acest lucru cu certitudine.până în prezent, am ajuns la concluzia că corelația populației nu este probabil zero. Aceasta este singura concluzie din abordarea ipotezei noastre nule și nu este chiar atât de interesantă.,ceea ce vrem cu adevărat să știm este corelația populației. Corelația eșantionului nostru de 0,25 pare o estimare rezonabilă. Noi numim un astfel de număr un singur punct de estimare.
acum, un nou eșantion poate veni cu o corelație diferită. O întrebare interesantă este cât de mult corelațiile noastre eșantion ar fluctua peste probe dacă am trage multe dintre ele. Figura de mai jos arată exact că, presupunând dimensiunea eșantionului nostru de N = 100 și estimarea noastră (punct) de 0,25 pentru corelația populației., 
intervale de încredere
rezultatul eșantionului nostru sugerează că aproximativ 95% din multe probe ar trebui să vină cu o corelație între 0,06 și 0,43. Acest interval este cunoscut ca un interval de încredere. Deși nu este exact corect, este cel mai ușor, deși de lățime de bandă, care este probabil să includă corelația populației.
un lucru de remarcat este că intervalul de concidență este destul de larg. Conține aproape o corelație zero, exact ipoteza nulă pe care am respins-o mai devreme.,
un alt lucru de remarcat este faptul că distribuția noastră de eșantionare și intervalul de încredere sunt ușor asimetrice. Ele sunt simetrice pentru cele mai multe alte statistici (cum ar fi mijloace sau coeficienți beta), dar nu corelații.