în aceste pagini ne uităm la câteva concepte interesante, ne uităm la spațiul curbat: ce înseamnă spațiul curbat, cum putem spune dacă un spațiu este curbat din interiorul sau din afara acestuia.ne uităm la modul în care putem încorpora pe tipul de spațiu în interiorul altul și a vedea că putem harta între spații diferite în moduri diferite.de asemenea, ne uităm la compactare și cum putem reprezenta vectori infinit de mari și infinitezimal mici în spațiile noastre în moduri care nu nu duc la singularități și alte probleme.,aceste concepte se dovedesc a fi utile, chiar și atunci când lucrăm cu spațiu plat, vom găsi modalități de a reprezenta vectori și planuri care nu trec prin origine. Acest lucru ne oferă modalități de a reprezenta rotațiile și traducerile ca o singură operație.cealaltă aplicație este spațiu-timp relativist.
Rienmannian Geometrie
În Rienmannian geometrie spațiu pot curba în diferite locuri (vezi colectoare) aici ne uităm la geometrii în cazul în care curba de spațiu este constantă.,
Eulidean Geometrie
spațiu plat
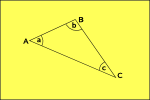
Geometrie Hiperbolica
spațiu curbele spre exterior
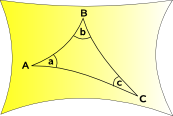
Geometrie Sferică și Eliptice Geometrie
spațiu curbe interior
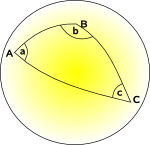
Într-o curbă (Non-Euclidiană) geometrie nu putem găsi un set de coordonate care sunt reciproc perpendiculare, unde coordona liniile sunt paralele între ele și în care fiecare pătrat de rețea are aceeași zonă., Am putea găsi, eventual, un sistem de coordonate în cazul în care putem face unele dintre acestea, dar nu toate.
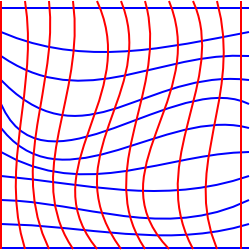
această diagramă încearcă să ilustreze această situație în 2 dimensiuni, deși este puțin înșelătoare, deoarece am desenat-o pe un plan, astfel încât am fi putut desena coordonate dreptunghiulare.pentru a încerca să ilustrăm o situație în care acest lucru este imposibil, ne-am putea gândi la un plan bidimensional care a fost întins în a treia dimensiune.,în această situație putem alege coordonatele care formează o grilă dreptunghiulară atunci când sunt proiectate pe un plan orizontal, cu toate acestea, pentru o persoană care trăiește la suprafață, atunci unele dintre pătratele grilei vor părea să aibă o suprafață mai mare decât altele, iar liniile grilei pot să nu pară paralele. Nu există un sistem de coordonate bidimensional care să păstreze simultan linii paralele, unghiuri și zone.,un exemplu similar este încercarea de a cartografia suprafața Pământului, putem folosi linii de latitudine și longitudine, dar liniile de longitudine se apropie mai aproape de poli.
în aceste cazuri am putea lucra în termeni de coordonate 3 dimensionale și aceasta este o abordare pe care o vom lua cu unele tipuri de geometrii non-euclidiene. Este adesea posibil să încorporați o anumită geometrie într-o Geometrie dimensională superioară pentru a o face mai euclidiană.,
uneori se întâmplă ca atunci când privim o geometrie la scară largă să nu fie euclidiană, dar dacă o privim la o scară din ce în ce mai mică, atunci ea se apropie de o geometrie euclidiană. Pentru a face acest lucru, trebuie să găsim un sistem de coordonate în care unghiurile sunt păstrate în fiecare punct, adică liniile de coordonate orizontale și verticale trebuie să se intersecteze întotdeauna la 90°, chiar dacă liniile nu pot fi drepte. Aceasta este cunoscută ca o geometrie conformă. În acest tip de geometrie putem defini cel puțin un sistem local de coordonate., legat de aceasta este dacă geometria poate fi diferențiată și integrată, o condiție pentru aceasta este că trebuie să se comporte bine și să nu aibă salturi bruște etc. Unele geometrii și sisteme de coordonate pot fi bine comportate în unele locuri, dar au singularități etc.
pentru discuții despre modul în care se măsoară curbura a se vedea această pagină.
notație matematică
cum facem față geometriilor unde nu putem folosi toate regulile care se aplică geometriei euclidiene?,
o abordare este utilizarea notației tensorilor, aceasta oferă convenții și notații care ne ajută în comutarea între diferite sisteme de coordonate. Un sistem ortogonal de coordonate, local în orice punct, poate fi definit prin utilizarea vectorilor de bază care sunt tangente la liniile de coordonate.,Galeriei
a se vedea această pagină
Relația dintre Hiperbolic și Minkowski Geometrii
| Minkowski Geometrie | Geometrie Hiperbolica | |
| punct | eveniment în spațiu-timp | particule în mișcare uniformă |
| distanța dintre două puncte | spațiu-intervalul de timp dintre două evenimente | viteza relativă între două astfel de particule |
Terminologie
Aici ne uităm la terminologie, cum ar fi geometriile, spații, modele, proiecții și transformă., Este destul de dificil atunci când începem să avem de-a face cu geometrii non-euclidiene, deoarece folosim o terminologie similară cu care suntem obișnuiți în spațiul Euclidian convențional, dar termenii pot avea proprietăți ușor diferite.,încerca
Eliptice Geometrie
Modele
Exemple sunt:
- Upper half-plane model
- Poincare disc model
- Proiective model
- Conforme modelului
Proiecțiile
Proiecție Stereografică
Transformă
Invariante
Exemple sunt:
- Möbius Transforma
- Lorentz Transforma
Postulatul
Dacă ne-am lua postulatul de Spațiu Euclidian.,acest lucru duce la:
- postulatul paralel este fals
- unghiurile unui triunghi nu se adaugă la π
- pentru o formă de dimensiune dată, nu există în general o formă similară de dimensiune mai mare.,ctive
conformal (Poincaré disc ) linii drepte – geodezice segmente de cercuri unghi păstra mai mult unghiurile interne ale triunghi π-(α+β+γ)=CΔ distanța dintre două puncte cu