rezolva ecuații numeric

găsiți toate rădăcinile unei funcții polinomiale

utilizați vpasolve pentru a găsi toate soluțiile funcției f(x)=6X7-2×6+3×3-8.

syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)

vpasolve se întoarce șapte rădăcini ale funcției, așa cum era de așteptat, pentru că funcția este un polinom de gradul șapte.,

Găsi Zerouri de un Nonpolynomial Folosind Funcția de Căutare, Variază și Puncte de Plecare

Un teren de funcția f(x)=e(x/7)cos(2x) relevă periodice zerouri, cu creșterea pârtiile de la zero puncte x crește.

syms xh = fplot(exp(x/7)*cos(2*x),);grid on

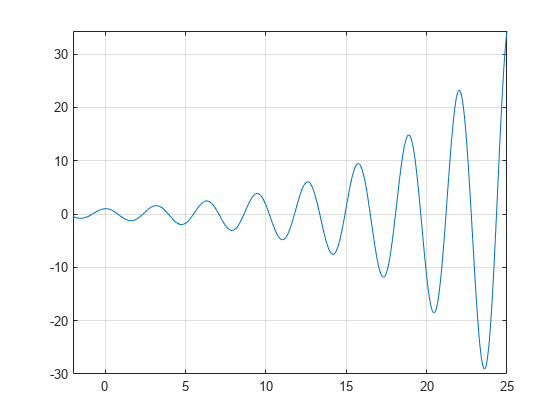
Utilizare vpasolve pentru a găsi un zerou al funcției f. Rețineți că vpasolve returnează o singură soluție a unei nonpolynomial ecuație, chiar dacă există mai multe soluții., On repeated calls, vpasolve returns the same result.

f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.

for k = 1:3 vpasolve(f,x,'Random',true)end

ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')

ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')

ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')

To find a zero close to x=10, set the starting point to 10.,

vpasolve(f,x,10)

ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')

Pentru a găsi aproape zero pentru x=1000, setați punctul de plecare pentru 1000.

vpasolve(f,x,1000)

ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')

Pentru a găsi zero în intervalul 15≤x≤25, setați intervalul de căutare pentru .,

vpasolve(f,x,)

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

Pentru a găsi mai multe zerouri în intervalul , nu poți să spui vpasolve în mod repetat pentru că ea returnează același rezultat pe fiecare apel, așa cum arătat anterior. În schimb, setați intervalul de căutare și setați 'Random' și true.,

for k = 1:3 vpasolve(f,x,,'Random',true)end

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')

'Random' selectează punctele de plecare aleatoriu, aceeași soluție ar putea fi găsit pe apeluri succesive.,

Găsi Toate Zerouri într-un anumit Interval de Căutare

Creați o funcție findzeros sistematică a găsi toate zerouri pentru f într-un anumit interval de căutare, într-o anumită toleranță la erori. Funcția începe cu intervalul de căutare de intrare și apelează vpasolve pentru a găsi un zero. Apoi, împarte intervalul de căutare în două în jurul valorii zero și se apelează recursiv cu noile intervale de căutare ca intrări pentru a găsi mai multe zerouri.

funcția este explicată secțiune cu secțiune aici.,

declarați funcția cu cele trei intrări și o ieșire. Prima intrare este funcția, a doua intrare este intervalul, iar a treia intrare opțională vă permite să specificați eroarea dintre un zero și limitele superioare și inferioare generate de acesta.

function sol = findzeros(f,range,err)

Dacă nu specificați argumentul opțional pentru toleranță la erori, findzeros seturi err și 0.001.

if nargin < 2 err = 1e-3;end

Găsi un zero în intervalul de căutare folosind vpasolve.,

sol = vpasolve(f,range);

Dacă vpasolve nu găsi un zero, ieșirea.

if(isempty(sol)) return

Dacă vpasolve găsește un zero, divizat în intervalul de căutare în două căutare variază de mai sus și mai jos de zero.

else lowLimit = sol-err; highLimit = sol+err;

apelfindzeros cu intervalul de căutare inferior. Dacă findzeros returnează zerouri, copiați valorile în matricea de soluții și sortați-le.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end

Apel findzeros cu cea mai mare gama de căutare., Dacă findzeros returnează zerouri, copiați valorile în matricea de soluții și sortați-le.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend

întregul funcția findzeros este după cum urmează. Salvați această funcție ca findzeros.m în folderul curent.

syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'

de a Obține Soluții la Precizie Arbitrară

Utilizare digits pentru a seta precizia de soluții returnate de către vpasolve., În mod implicit, vpasolve returnează soluții la o precizie de 32 de cifre semnificative.

f = exp(x/7)*cos(2*x);vpasolve(f)

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

Utilizare digits pentru a crește precizia de 64 de cifre semnificative. Când modificați digits, asigurați-vă că salvați valoarea curentă, astfel încât să o puteți restaura.,

digitsOld = digits;digits(64)vpasolve(f)

ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')

apoi, schimba precizia de soluții pentru 16 cifre semnificative.

digits(16)

rezolvați ecuațiile Multivariate folosind intervale de căutare

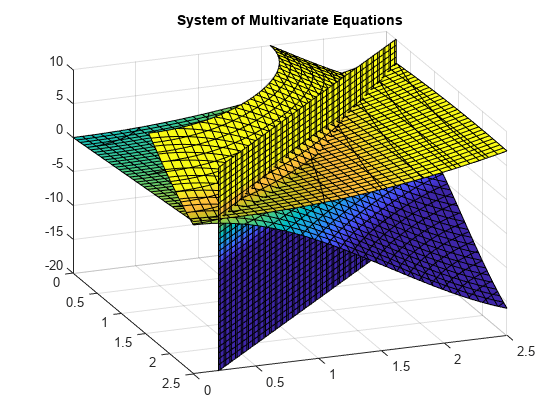
luați în considerare următorul sistem de ecuații.

Un teren de ecuații pentru 0≤x≤2,5 și 0≤x≤2.5 arată că cele trei suprafețe se intersectează în două puncte., Pentru a vizualiza mai bine complotul, utilizați view. Pentru a scala valorile colormap, utilizați caxis.

Utilizare vpasolve pentru a găsi un punct în cazul în care suprafețele care se intersectează. Funcția vpasolve returnează o structură. Pentru a accesa x-, y și z-valori de soluție, indicele în structura.,

sol = vpasolve(equations);

pentru a căuta o regiune a spațiului soluției, specificați intervalele de căutare pentru variabile. Dacă specificați intervalele 0≤x≤1.5 și 1.5≤y≤2.5, atunci funcția vpasolve caută zona delimitată afișată.

Utilizare vpasolve pentru a găsi o soluție pentru acest domeniu de căutare. Pentru a omite un interval de căutare pentru z, setați al treilea interval de căutare la .,pentru a găsi mai multe soluții, setați opțiunea 'Random' la true. Acest lucru face ca vpasolve să utilizeze puncte de pornire aleatorii pe rulări succesive. Opțiunea 'Random'poate fi utilizată împreună cu intervalele de căutare pentru a facevpasolve să utilizeze puncte de pornire aleatorii într-un interval de căutare. Deoarece 'Random' selectează aleatoriu punctele de pornire, aceeași soluție poate fi găsită la apelurile succesive., Apel vpasolve în mod repetat pentru a vă asigura că găsiți ambele soluții.

trasează ecuațiile. Suprapune soluții ca un scatter plot de puncte cu galben X markeri folosind scatter3. Pentru a vizualiza mai bine complotul, faceți două dintre suprafețe transparente folosind alpha. Scala colormap la complot valori folosind caxis, și de a schimba perspectiva, folosind view.

vpasolve găsește soluții la intersecția suprafețelor formate de ecuații așa cum se arată.,

Lastly, restore the old value of digits for further calculations.

digits(digitsOld)