proprietățile zonelor
Centroid
centroidul unei forme reprezintă punctul despre care zona secțiunii este distribuită uniform. Dacă zona este dublu simetrică în jurul a două axe ortogonale, centroidul se află la intersecția acestor axe. Dacă zona este simetrică în jurul unei singure axe, atunci centroidul se află undeva de-a lungul acelei axe (cealaltă coordonată va trebui calculată)., Dacă locația exactă a centrului de greutate nu poate fi determinată prin inspecție, poate fi calculată prin:
|
|
|
unde dA reprezintă zona de un infinit de mic element, a este aria totală a secțiunii transversale, iar x și y sunt coordonatele elementului dA în raport cu axa de interes.,locațiile centroidale ale secțiunilor transversale comune sunt bine documentate, deci de obicei nu este necesar să se calculeze locația cu ecuațiile de mai sus., de forme de bază ale căror centroidal locații sunt cunoscute cu privire la un punct de referință, atunci centroidal locul de compozit secțiune transversală poate fi calculată ca:
|
|
|
în cazul în care xc,am si yc,eu sunt coordonatele rectangulare ale centroidal locația cu secțiunea în raport cu punctul de referință, iar Ai-ul este zona cu secțiune.,
distanța Centroidală
distanța centroidală, c, este Distanța de la centroidul unei secțiuni transversale la fibra extremă., La centroidal distanța în y-direcția pentru o secțiune dreptunghiulară este prezentată în figura de mai jos:
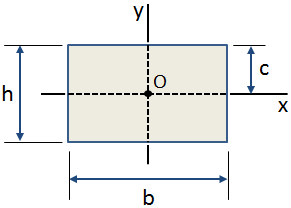
utilizări Comune pentru centroidal distanța include:
- calculul valorii maxime de stres îndoire într-o secțiune transversală
- calcularea valorii de primul moment de zona, Q, mai sus un punct din secțiunea transversală a determina tensiunea de forfecare la acest punct
Avem o serie de probleme structurale calculatoare pentru a alege de la.,
- Beam Calculator
- Suruburi Comun Calculator
- Bolt Model de Distribuție a Forței
- Lug Calculator
- Coloana de Flambaj Calculator
- Fisurilor de Oboseală Calculator

Primul Moment al Zonei
primul moment dintr-o zonă în raport cu axa de interes este calculat ca:
| Qx = ∫ y dA | Aa = ∫ x dA |
unde Qx este primul moment despre x-axa Qy este primul moment în jurul axei y.,Dacă zona este compus dintr-o colecție de forme de bază ale căror centroidal locații sunt cunoscute în raport cu axa de interes, apoi primul moment de compozit zona poate fi calculată ca:
|
|
|
Rețineți că primul moment al zonei este folosit atunci când se calculează centrul de greutate de o secțiune cu privire la unele origine (cum s-a discutat anterior)., Primul moment este de asemenea utilizat la calcularea valorii tensiunii de forfecare la un anumit punct din secțiunea transversală. În acest caz, primul moment este calculat pentru o zonă care constituie o porțiune mai mică a secțiunii transversale, unde zona este limitată de punctul de interes și de fibra extremă (de sus sau de jos) a secțiunii transversale. Primul moment este calculat în jurul unei axe care trece prin centroidul secțiunii transversale.,
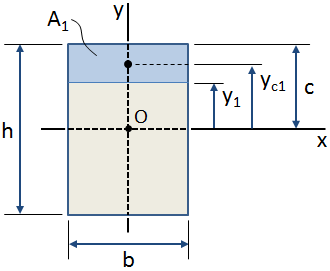
În figura de mai sus, umbrită albastru zonă este zona de maxim interes general secțiune transversală.,nt de acest domeniu în raport cu axa x (care trece prin secțiunea transversală centrul de greutate, punctul O din figura de mai sus) se calculează ca:
Dacă centroidal locația din zona de interes este cunoscut, apoi primul moment de zona în raport cu axa poate fi calculată ca (consultați figura de mai sus):
ar trebui să fie remarcat faptul că primul moment dintr-o zonă va fi pozitivă sau negativă în funcție de poziția zonei față de axa de interes., Prin urmare, primul moment al întregii zone a unei secțiuni transversale în raport cu propriul centroid va fi zero.
zona momentul de inerție
al doilea moment al zonei, mai cunoscut sub numele de momentul de inerție, I, al unei secțiuni transversale este o indicație a capacității unui element structural de a rezista la îndoire.,(Nota 1), Ix și Iy sunt momentele de inerție despre x – și y – axe, respectiv, și se calculează prin:
| Ix = ∫ y2 dA | Iy = ∫ x2 dA |
în cazul în care x și y sunt coordonatele elementului dA în raport cu axa de interes.cel mai frecvent, momentele de inerție sunt calculate în raport cu centroidul secțiunii. În acest caz, ele sunt denumite momente centroidale de inerție și sunt notate ca Icx pentru inerția despre axa x și Icy pentru inerția despre axa Y.,momentele de inerție ale secțiunilor transversale comune sunt bine documentate, deci de obicei nu este necesar să le calculăm cu ecuațiile de mai sus. Proprietățile mai multor secțiuni transversale comune sunt date la sfârșitul acestei pagini.dacă o secțiune transversală este compusă dintr-o colecție de forme de bază ale căror centroizi coincid, atunci momentul de inerție al secțiunii compozite este pur și simplu suma momentelor individuale de inerție. Un exemplu în acest sens este un fascicul de cutie care constă din două secțiuni dreptunghiulare, așa cum se arată mai jos., În acest caz, secțiunea exterioară are „zonă pozitivă”, iar secțiunea interioară are „zonă negativă”, astfel încât momentul compozit de inerție este scăderea momentului de inerție a secțiunii interioare din secțiunea exterioară.
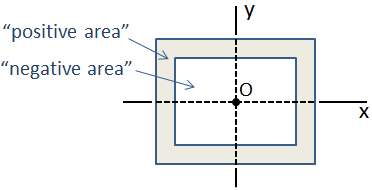
În cazul mai complicat compozite cu secțiunea transversală în care centroidal locații nu sunt coincidente, momentul de inerție poate fi calculată folosind în paralel axei teorema.este important să nu confundăm momentul inerției unei zone cu momentul de masă al inerției unui corp solid., Momentul zonei de inerție indică rezistența unei secțiuni transversale la încovoiere, în timp ce momentul masei de inerție indică rezistența unui corp la rotație.,
Axă Paralelă Teorema
Dacă momentul de inerție al o secțiune despre un centroidal axa este cunoscut, atunci axă paralelă teorema poate fi folosit pentru a calcula momentul de inerție față de orice axă paralelă:
unde Ic este momentul de inerție despre centroidal axa, d este distanța dintre centroidal axe și paralele axei, și O este aria secțiunii transversale.,
Dacă o secțiune transversală este compus dintr-o colecție de forme de bază ale căror centroidal momente de inerție sunt cunoscute împreună cu distanțele dintre centrele de greutate la un punct de referință, atunci axă paralelă teorema poate fi folosit pentru a calcula momentul de inerție al compozite secțiune transversală.de exemplu, un fascicul I poate fi aproximat cu 3 dreptunghiuri, după cum se arată mai jos. Deoarece această secțiune compozită este simetrică atât în ceea ce privește axele x, cât și y, centroidul secțiunii poate fi localizat prin inspecție la intersecția acelor axe. Centroidul este situat la originea, O, în figură.,
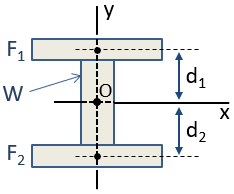
momentul de inerție al compozite secțiune poate fi calculată cu ajutorul axă paralelă teorema. Momentul centroidal de inerție al secțiunii în jurul axei X, Icx, este calculat ca:
unde Icx termeni sunt momentele de inerție ale secțiunilor individuale cu privire la propria lor centroizi în orientarea axei x, d termeni sunt distanțele de la secțiunea individual centroizi să compozit secțiunea centrul de greutate, iar termenii sunt ariile secțiunilor individuale. Deoarece centroidul secțiunii W și centroidul secțiunii compozite coincid, d este zero pentru acea secțiune și deci nu există un termen Ad2.,este important de observat implicația teoremei axei paralele că, pe măsură ce o secțiune individuală se deplasează mai departe de centroidul secțiunii compozite, contribuția acelei secțiuni la momentul de inerție al secțiunii compozite crește cu un factor de d2. Prin urmare, dacă intenția este de a crește momentul de inerție al unei secțiuni despre o anumită axă, este cel mai eficient să localizați zona cât mai departe de axa respectivă. Aceasta explică forma unui fascicul I., Flanșele sunt principalii contribuitori la momentul inerției, iar pânza servește la separarea flanșelor de axa de îndoire. Web are nevoie pentru a menține o anumită grosime, cu toate acestea, pentru a evita flambaj și pentru că web are o parte semnificativă a stresului de forfecare în secțiunea.
momentul Polar de inerție
momentul polar de inerție, I, al unei secțiuni transversale este o indicație a capacității unui element structural de a rezista la torsiune în jurul unei axe perpendiculare pe secțiune., La momentul de inerție polar pentru o secțiune în raport cu axa care poate fi calculată prin:
în cazul în care x și y sunt coordonatele elementului dA în raport cu axa de interes, iar r este distanța între element dA și axa de interes.,
Deși momentul de inerție polar poate fi calculată cu ajutorul ecuației de mai sus, este de obicei mai convenabil pentru a calcula folosind axe perpendiculare teorema care afirmă că momentul de inerție polar al unei zone este suma momentelor de inerție față de două axe ortogonale care trec prin axa de interes:
cel Mai frecvent, axa de interes trece prin centrul de greutate al secțiunii transversale.,
Secțiunea Modul
maximul de stres îndoire într-un fascicul se calculează ca unde σb = Mc / Ic, unde c este distanța de la axa neutră la fibra extremă, Icis la centroidal momentul de inerție, iar M este momentul încovoietor. La secțiunea modul combină c și Ic termenii din incovoiere ecuația:
Folosind secțiunea modul, presiunea la incovoiere este calculat ca unde σb = M / S. utilitatea secțiunea modul este că ea caracterizează rezistența la îndoire de o secțiune transversală într-un singur termen., Acest lucru permite optimizarea secțiunii transversale a unui fascicul pentru a rezista la îndoire prin maximizarea unui singur parametru.
raza girației
raza girației reprezintă distanța de la centroidul unei secțiuni la care toată zona ar putea fi concentrată fără a avea niciun efect asupra momentului de inerție.,>
A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:
The rectangular radii of gyration can also be used to calculate the polar radius of gyration:
We have a number of structural calculators to choose from., Aici sunt doar câteva:
- Beam Calculator
- Suruburi Comun Calculator
- Bolt Model de Distribuție a Forței
- Lug Calculator
- Coloana de Flambaj Calculator
- Fisurilor de Oboseală Calculator

Proprietăți Comune Secțiunilor
tabelul De mai jos oferă proprietăți comune secțiunilor transversale. Tabele mai extinse pot fi găsite în referințele enumerate.proprietățile calculate în tabel includ aria, momentul centroidal de inerție, modulul secțiunii și raza girației.,
avem un număr de calculatoare structurale pentru a alege de la., Aici sunt doar câteva:
- Beam Calculator
- Suruburi Comun Calculator
- Bolt Model de Distribuție a Forței
- Lug Calculator
- Coloana de Flambaj Calculator
- Fisurilor de Oboseală Calculator

Note
Nota 1: Devierea unui Fascicul
devierea unui fascicul sub îndoire este determinat de momentul de inerție al secțiunii transversale, lungime de unda, iar modulul de elasticitate al materialului. Mai multe detalii sunt date în această discuție despre deformarea fasciculului.