Să începem cu un exemplu simplu, să spunem că vrem să multiplicăm (2x-3)3. Acest lucru nu ar fi prea dificil de a face mână lungă, dar să folosim teorema binomului, astfel încât atunci când întâlniți extinderi mai mari, cum ar fi binomiile ridicate la puterile 4, 5, 6, … veți ști exact ce să faceți.pentru a începe, trebuie să identificați cei doi termeni din binomul dvs. (pozițiile x și y ale formulei noastre de mai sus) și puterea (n) la care extindeți binomul.,
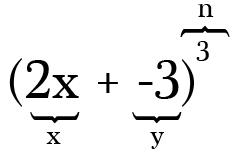
De exemplu, pentru a extinde (2x-3)3, cei doi termeni sunt 2x și -3 și puterea, sau n valoare, este de 3. Rețineți că ori de câte ori aveți o scădere în binomul dvs., este atât de important să vă amintiți să includeți minusul ca simbol negativ pe termenul însoțitor.lucrul minunat despre teorema binomială este că ne permite să găsim polinomul extins fără a înmulți împreună o grămadă de binomiale. Destul de elegant, nu?, Se pare că numărul de termeni din polinomul dvs. extins va fi întotdeauna unul mai mult decât puterea pe care o extindeți. Asta înseamnă că vom crea un polinom cu 4 termeni, deoarece puterea din acest exemplu este 3.
fiecare termen va avea o (2x) și (-3), precum și „n alege k” formula unde n=3. Puteți merge mai departe și scrie că în jos de 4 ori, unul pentru fiecare termen, lăsând valoarea k în „n alege k” și puterile necompletate pentru moment.
în continuare veți dori să completați k-valori și puteri. Aici puteți urma formula de însumare, crescând puterea pentru fiecare termen., Dar este destul de ușor să urmezi doar tiparele.valorile k din „n choose k”, vor începe cu k=0 și vor crește cu 1 în fiecare termen. Ultimul termen ar trebui să se încheie cu n egal cu k, în acest caz n=3 și k=3.
apoi trebuie să adăugăm puterile pe (2x) și (-3).
power on (2x) va începe cu valoarea n, deci în acest caz 3, și va scădea cu 1 pe fiecare termen, până când ajungeți la zero. Pornirea (-3) va începe cu zero și va crește de fiecare dată până când ajungeți la n sau 3 în această problemă.,

Pentru orice valoare a ridicat la puterea zero este egal cu 1, puteți simplifica termenii cu puteri de la zero.

Apoi mergeți mai departe și de a aplica competențele și de a simplifica oriunde este posibil.,

Triunghiul lui Pascal comenzi rapide

ultima parte este de a rezolva combinații formula. Modul evident de a face acest lucru este de a aplica formula combinațiilor pentru fiecare problemă. Dar vom lua o scurtătură drăguță aici folosind triunghiul lui Pascal.triunghiul lui Pascal este un triunghi simplu, dar puternic format prin crearea unui triunghi cu trei 1-uri pentru a începe., Pentru fiecare rând după aceea, pur și simplu scrieți 1 pe ambele capete și găsiți numărul(numerele) din mijloc adăugând cele două valori direct deasupra acestuia.

Acum, aici e partea bună. Ascunse în triunghiul lui Pascal sunt toate răspunsurile la orice „N alege k”! E ca o mica inselatorie secreta!diagrama de mai jos vă arată unde se află „n choose k ‘s” ascuns.,

Pentru problema noastră avem nevoie pentru a rezolva pentru: 3 alege 0, 3 alege 1, 3 alege 2, și 3 alege 3. Care sunt toate valorile din rândul 4. Deci, tot ce trebuie să facem este să ne uităm la al 4-lea rând al triunghiului lui Pascal și să potrivim răspunsurile.
al 4-lea rând are valorile: 1, 3, 3, 1. Așa că voi înlocui răspunsurile pentru n-urile noastre.,

în cele din Urmă, tot ce trebuie să faceți este de a se multiplica și de a simplifica fiecare termen până la forma sa cea mai simplă. Nu uitați să verificați răspunsul final pentru a vă asigura că puterile pe fiecare termen se adaugă în continuare la gradul binomului original! Crede-mă, e incredibil de ușor de a face o greșeală de transcriere în acest tip de problema 😉
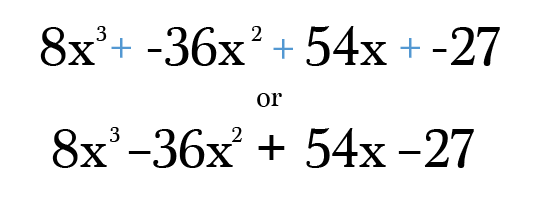
Nevoie de un alt exemplu?,
în videoclipul de mai sus, vă arăt cum să utilizați teorema binomială pentru a extinde binomul (x – 3y)⁵. În plus, vă arăt câteva trucuri suplimentare pentru a rămâne organizat și câteva verificări rapide pe care le puteți utiliza pentru a identifica cu ușurință erorile comune.
Vă mulțumim pentru lectură!
❤ rămâneți conectat ❤
rămâneți la curent cu tot ceea ce este de până la Math Hacks!