Zăpadă la peste temperaturi de îngheț

V-ați întrebat vreodată cum e zapada la peste temperaturi de îngheț? Ei bine, explicația naivă este că pur și simplu este nevoie de timp pentru ca fulgii de zăpadă să se topească odată ce pătrund deasupra aerului înghețat, în timp ce coboară în jos la pământ. Acesta este, desigur, motivul pentru care grindina poate cădea pe vreme caldă. Pur și simplu, pietrele de grindină cad repede, prea repede pentru a lăsa aerul cald să topească grindina. Aceasta nu este însă principala explicație pentru motivul pentru care poate ninge atunci când este peste îngheț.,
din figura de mai jos, este evident că există o dependență clară de umiditate – cu cât este mai uscată, cu atât mai caldă poate fi în timp ce ninge. Acest lucru implică faptul că principalul factor, cel puțin în condiții uscate, are legătură cu umiditatea. Și acest factor este evaporarea. Mai exact, pe măsură ce fulgii de zăpadă coboară, se evaporă. Acest proces ia căldură și menține fulgii la rece.
astfel, dacă dorim să calculăm temperatura maximă, trebuie să estimăm echilibrul termic net al fulgului. În primul rând, pe măsură ce fulgii călătoresc într-un mediu cald, câștigă căldură din jur prin conducere., În al doilea rând, căldura este utilizată pentru a evapora fulgii, răcindu-i astfel. Dacă căldura de evaporare „chiuveta” este mai mare decât conducta de căldură, fulgii vor rămâne înghețați.
Se pare că acest lucru poate fi ușor calculat. Nu, nu este simplu să se calculeze conducta de căldură sau căldura de evaporare, dar raportul este, deoarece diferiți factori geometrici necunoscuți se anulează.
dacă nu vă pasă de calcul (pentru că nu sunteți un ciudat științific), puteți vizita pur și simplu pagina calculatorului.
dacă vă pasă, aici este derivarea., Să presupunem că fluxul în jurul fulgilor este astfel încât în jurul acestuia se formează un strat limită de lățime D. Totalul fluxului de căldură $F_H$ la fulg (de exemplu, J/sec în MKS) va fi dată de legea lui Fourier:

unde $\kappa$ este de căldură coeficient de difuzie a aerului (de exemplu, m2/sec în MKS), c este capacitatea termică a aerului (J/kg în MKS), A este suprafața stratului limită în jurul fulg, iar ΔT este diferența de temperatură între fulg și mediu.,
în mod Similar, se poate folosi legea lui Fick pentru a obține difuzia vaporilor de apă din fulg (unde temperatura este aproape de zero, iar umiditatea relativă este de 100%), a mediului înconjurător, în cazul în care temperatura este mai ridicată și umiditatea relativă a aerului mai mică:

aici, D este coeficientul de difuzie a apei (de exemplu, m2/sec în MKS) și ρ este densitatea vaporilor de apă (kg/m3 în MKS).,
evaporarea gheață necesită căldură, astfel, dacă există o vapori de apă de masă fluxul Φ de fulg, ar fi nevoie de căldură, la o rata de $F_w = \epsilon \Phi$ unde $\epsilon$ este căldura de vaporizare de gheață (J/kg în MKS).
Cea mai mare temperatura peste care fulg de nea se topeste, este temperatura pentru care cele două fluxurile de căldură sunt egale:

rețineți că geometria fluxului în jurul fulgului anulează, deoarece ambele fluxuri de căldură depind de d și A în același mod., Acesta ar fi cazul și dacă stratul limită din jurul fulgului este complex, astfel încât d depinde de fapt de direcție. Prin urmare,

unde $\rho_{sat}$ este densitatea vaporilor de apă de saturație.
conectarea numerelor (care pot fi găsite, de exemplu, în manualul CRC de chimie și fizică), rezultă cu o ecuație implicită pentru temperaturădeoarece densitatea vaporilor de apă de saturație depinde și de temperatură., Putem simplifica lucrurile dacă ne întrebăm în schimb care este umiditatea relativă necesară pentru a menține fulgul înghețat la o temperatură dată. Este:

unde $t_c$ este temperatura în grade Celsius.
această funcție poate fi văzută în figura de mai jos, împreună cu datele de la Matsuo și Sasyo, 1981. După cum se poate observa din figură, graficul calculat este aproximativ limita inferioară sub care nu există nici un fel de ploaie. La temperaturi mai calde, există un amestec., Până la aproximativ 1°C deasupra liniei fără topire, există cea mai mare parte zăpadă, în timp ce între aproximativ 1°C și 2°C deasupra liniei, este în mare parte ploaie, dar zăpada este posibilă. Aceste evenimente s-ar putea datora unor efecte suplimentare, cum ar fi scăderi puternice, timpul necesar pentru topirea zăpezii etc.

zăpadă sau ploaie? Linia roșie este linia fără topire. Sub ea, fulgii de zăpadă se răcesc prin evaporare mai mult decât se încălzesc din mediul înconjurător, menținându-se astfel înghețați. Magneta și liniile albastre sunt +1°C și +2°C deasupra liniilor fără topire., Între 0°C și +1°C deasupra liniei fără topire, ninge în cea mai mare parte, în timp ce plouă în cea mai mare parte între +1°C și +2°C deasupra liniei fără topire. La temperaturi mai calde, plouă. Punctele verzi sunt evenimente colectate de Matsuo și Sasyo (1981) în Wajima Japonia, între 1975 și 1978. astfel, dacă dorim să observăm zăpadă caldă, sunt necesare condiții foarte uscate. De exemplu, dacă umiditatea solului este de aproximativ 20% (foarte rar, deoarece dacă există precipitații, atmosfera este în general umedă!) apoi ar putea ninge la 8°C (sau 46 ° F pentru utilizatorii englezi).,
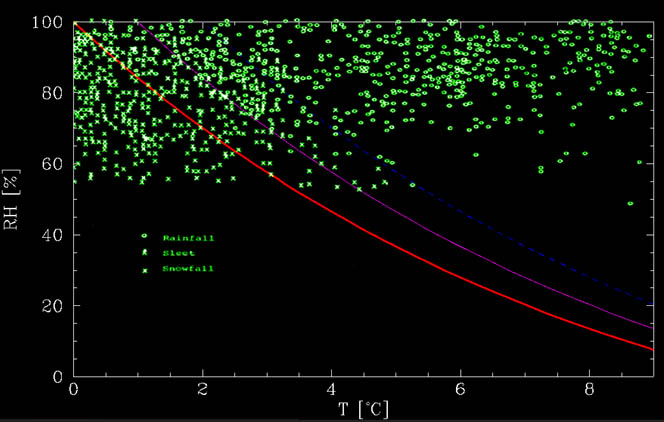
O altă cerință este ca nicăieri de-a lungul coborârii aerul să nu depășească linia fără topire. Dacă se întâmplă, fulgul se va topi, desigur.
dacă temperatura crește peste îngheț, nu există parametri cu care tipul de precipitații poate fi determinat pentru certitudine. Tot ce putem prezice atunci este probabilitatea ca zăpada să cadă de fapt. Acest lucru se poate face folosind rezultatele häggmark și Ivarsson (1997), corectate numai pentru a utiliza becul înghețat și nu temperatura becului umed.
linia de jos este un calculator cu care se poate estima probabilitatea zăpezii.,

cum este legată de temperatura becului umed? Relația dintre temperatura pe care o găsim și temperatura de îngheț a apei este foarte asemănătoare cu relația dintre becul uscat și temperaturile becului web (unde acesta din urmă este temperatura redusă pe care un termometru umed o va citi din cauza evaporării apei). Principala diferență este că temperatura bulbului umed include evaporarea apei, în timp ce în cazul nostru este evaporarea gheții, cu 15% mai multă pierdere de energie. Astfel, căutăm în esență temperatura becului uscat pentru care temperatura becului „înghețat” este de 0°C.