
Haben Sie sich jemals gefragt, wie es bei Temperaturen über dem Gefrierpunkt schneien kann? Nun, die naive Erklärung ist, dass es einfach Zeit braucht, bis die Schneeflocken schmelzen, sobald sie über dem Gefrierpunkt Luft durchdringen, während sie nach unten auf den Boden absteigen. Dies ist natürlich der Grund, warum Hagel bei warmem Wetter fallen kann. Einfach, Hagelsteine fallen schnell, zu schnell, um die warme Luft den Hagel schmelzen zu lassen. Dies ist jedoch nicht die Haupterklärung dafür, warum es schneien kann, wenn es über dem Gefrierpunkt liegt.,
Aus der folgenden Abbildung geht hervor, dass es eine klare Abhängigkeit von der Luftfeuchtigkeit gibt – je trockener es ist, desto wärmer kann es beim Schneien sein. Dies bedeutet, dass der Hauptfaktor, zumindest bei trockenen Bedingungen, mit Feuchtigkeit zu tun hat. Und dieser Faktor ist Verdunstung. Genauer gesagt, wenn die Schneeflocken absteigen, verdampfen sie. Dieser Prozess nimmt Wärme auf und hält die Flocken kalt.
Also, wenn wir die maximale Temperatur berechnen möchten, müssen wir die Nettowärmebilanz der Flocke schätzen. Erstens, wenn sich die Flocken in einer warmen Umgebung bewegen, gewinnen sie Wärme aus der Umgebung durch Leitung., Zweitens wird Wärme verwendet, um die Flocken zu verdampfen und dadurch abzukühlen. Wenn die Verdampfungswärme „sinken“ größer als die Wärmeleitung ist, bleiben die Flocken gefroren.
Es stellt sich heraus, dass dies leicht berechnet werden kann. Nein, es ist nicht einfach, die Wärmeleitung oder die Verdampfungswärme zu berechnen, sondern das Verhältnis ist, da verschiedene unbekannte geometrische Faktoren aufheben.
Wenn Sie sich nicht um die Berechnung kümmern (weil Sie kein Wissenschaftsfreak sind), können Sie einfach die Rechnerseite besuchen.
Wenn Sie kümmern, hier ist die Ableitung., Angenommen, die Strömung um die Flocken ist so, dass sich eine Grenzschicht der Breite d bildet. Der Gesamtwärmefluss $F_H$ zur Flocke (z. B. J/sec in MKS) wird durch das Fourier-Gesetz gegeben:
wobei $\kappa$ der Wärmediffusionskoeffizient von Luft ist (z. B. m2/sec in MKS), c die Wärmekapazität von Luft ist (J/kg in MKS), A die Oberfläche der Grenzschicht um die Flocke ist, während ΔT ist die Temperaturdifferenz zwischen der Flocke und der Umgebung., In ähnlicher Weise kann man das Fick-Gesetz verwenden, um die Diffusion von Wasserdampf von der Flocke (wo die Temperatur nahe dem Gefrierpunkt liegt und die relative Luftfeuchtigkeit 100% beträgt) in die Umgebung zu erhalten, wo die Temperatur höher und die relative Luftfeuchtigkeit niedriger ist:
Hier ist D der Wasserdiffusionskoeffizient (z. B. m2 / sec in MKS) und ρ die Wasserdampfdichte (kg/m3 in MKS).,
Das verdampfende Eis benötigt Wärme, also, wenn es einen Wasserdampfmassenfluss von Φ von der Flocke gibt, würde es Wärme mit einer Rate von $F_w = \epsilon \Phi$ erfordern, wobei $\epsilon$ die Verdampfungswärme von Eis ist (J/kg in MKS).
Die höchste Temperatur, oberhalb derer die Schneeflocke schmilzt, ist die Temperatur, für welche die beiden wärmeströme sind die gleich: „
Beachten Sie, dass sich die Geometrie der Strömung um die Flocke auflöst, da beide Wärmeflüsse auf dieselbe Weise von d und A abhängen., Dies wäre auch dann der Fall, wenn die Grenzschicht um die Flocke so komplex ist, dass d tatsächlich von der Richtung abhängt. Daher,
wobei $\rho_{sat}$ die Sättigungswasserdampfdichte ist.
Das Einstecken der Zahlen (die zum Beispiel im CRC handbook of chemistry and physics zu finden sind) führt zu einer impliziten Gleichung für die Temperaturweil die Sättigungswasserdampfdichte auch von der Temperatur abhängt., Wir können die Dinge vereinfachen, wenn wir stattdessen fragen, wie hoch die relative Luftfeuchtigkeit ist, um die Flocke bei einer bestimmten Temperatur gefroren zu halten. Es ist:
wobei $T_C$ die Temperatur in Grad Celsius ist.
Diese Funktion ist in der folgenden Abbildung zusammen mit Daten von Matsuo und Sasyo, 1981, zu sehen. Wie aus der Abbildung ersichtlich, ist die berechnete Grafik ungefähr die untere Grenze, unter der es überhaupt keinen Regen gibt. Bei wärmeren Temperaturen gibt es eine Mischung., Bis etwa 1°C oberhalb der Schmelzlinie liegt meist Schnee, während es zwischen etwa 1°C und 2°C oberhalb der Linie meist regnet, aber Schnee möglich ist. Diese Ereignisse können auf zusätzliche Effekte zurückzuführen sein, z. B. starke Fallstricke, Zeit zum Schmelzen des Schnees usw.
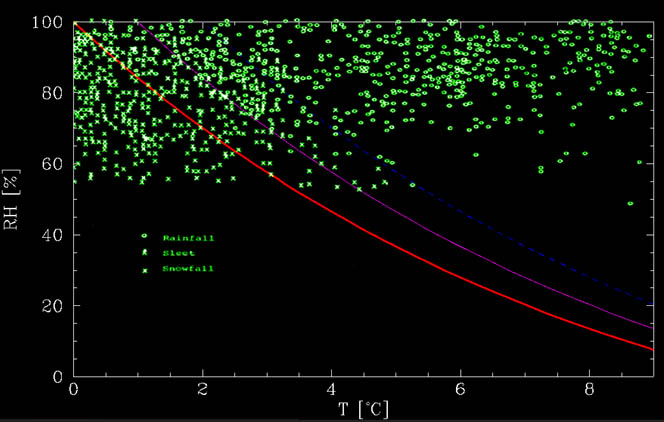
Wenn wir also warmes Wetter Schnee beobachten möchten, sind sehr trockene Bedingungen erforderlich. Zum Beispiel, wenn die Bodenfeuchtigkeit nur etwa 20% beträgt (sehr selten, denn wenn es Niederschlag gibt, ist die Atmosphäre im Allgemeinen nass!) dann könnte es bei 8°C (oder 46°F für englische Benutzer) schneien.,
Eine weitere Anforderung ist, dass nirgendwo entlang des Abstiegs die Luft die No-Melt-Linie übertrifft. Wenn dies der Fall ist, wird die Flocke natürlich schmelzen.
Wenn die Temperatur über den Gefrierpunkt steigt, gibt es keine Parameter, mit denen die Art des Niederschlags mit Sicherheit bestimmt werden kann. Alles, was wir dann vorhersagen können, ist die Wahrscheinlichkeit, dass tatsächlich Schnee fällt. Dies kann anhand der Ergebnisse von Häggmark und Ivarsson (1997) erfolgen, die nur korrigiert wurden, um die gefrorene Glühbirne und nicht die Temperatur der feuchten Glühbirne zu verwenden.
unterm Strich ist ein Rechner, mit dem die Wahrscheinlichkeit von Schnee geschätzt werden kann.,