aloitetaan suoraviivaisella esimerkillä, sanotaan, että haluamme moninkertaistaa (2x-3) 3. Tämä ei olisi liian vaikea tehdä pitkän käsi, mutta katsotaanpa käyttää binomisen lause niin, että kun kohtaat suurempia laajennuksia, kuten binomials nostetaan 4, 5, 6, … voimia tiedät tarkalleen, mitä tehdä.
päästä alkuun, sinun täytyy tunnistaa kaksi ehdot sinun binomi (x-ja y kantoja meidän kaava edellä) ja voima (n) olet laajentaminen binomial mukaan.,
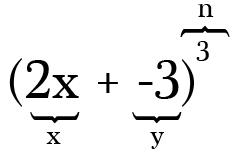
esimerkiksi, laajentaa (2x-3)3, kaksi termiä ovat 2 ja -3 ja valtaa, tai n: n arvo on 3. Huomaa, että kun sinulla on vähennys oman binomisen se on niin tärkeää muistaa sisällyttää miinus negatiivinen symboli mukana aikavälillä.
ihana asia, noin binomisen lause on se antaa meille mahdollisuuden löytää laajeni polynomi ilman kertomalla joukko binomials yhdessä. Aika siistiä, eikö?, Käy ilmi, että termien määrä laajennetussa polynomissa on aina yksi enemmän kuin voima, jota laajennat. Se tarkoittaa, että luomme polynomin 4 termillä, koska voima tässä esimerkissä on 3.
jokaisella termillä on a (2x) ja (-3) sekä ”n valitse k” formula_3. Voit mennä eteenpäin ja kirjoittaa, että alas 4 kertaa, yksi kutakin aikavälillä, jolloin k-arvo ”n choose k” ja valtuudet tyhjä tällä hetkellä.
seuraavaksi haluat täyttää k-arvot ja voimat. Täällä voit seurata summaus kaava, lisäämällä valtaa kunkin termin., Kuvioiden seuraaminen on kuitenkin aika helppoa.
k-arvoja ”n choose k”, alkaa k=0, ja kasvaa 1 kunkin aikavälillä. Viimeinen termi pitäisi päättyä n yhtä k, tässä tapauksessa n=3 ja k=3.
seuraavaksi pitää lisätä voimat (2x) ja (-3).
virta päällä (2x) alkaa n-arvolla, joten tässä tapauksessa 3, ja vähenee 1 kullakin aikavälillä, kunnes pääset nollaan. Virta päälle (-3) on aluksi nolla ja kasvaa yhdellä joka kerta, kunnes saat n tai 3 tässä ongelma.,

Koska mitään arvoa nostetaan nolla, voima on yhtä suuri kuin 1, voit yksinkertaistaa ehdot, joilla on valtuudet nolla.

Seuraavaksi mennä eteenpäin ja käyttää toimivaltuuksia ja yksinkertaistaa mahdollisuuksien mukaan.,

Pascalin Kolmio Pikakuvake

viimeinen osa on ratkaista yhdistelmiä kaava. Ilmeinen tapa tehdä tämä on soveltaa yhdistelmiä kaava kunkin ongelma. Menemme oikotietä käyttäen Pascalin kolmiota.
Pascalin Kolmio on yksinkertainen, mutta tehokas kolmio muodostuu luoda kolmio, jossa on kolme 1: n alkavan., Kunkin rivin jälkeen yksinkertaisesti kirjoittaa 1: n molemmissa päissä, ja löytää keskimmäinen numero(T) lisäämällä kaksi arvoa suoraan sen yläpuolella.

Nyt tässä on hyvä osa. Piilotettu Pascalin kolmion ovat kaikki vastaukset tahansa ”n valita k”! Se on kuin salainen pikku cheatsheet!
alla Oleva kaavio näyttää missä piilotettu ”n choose k” sijaitsevat.,

– meidän ongelma, joka meidän täytyy ratkaista: 3 valitse 0, 3 valita 1, 3 valitse 2, ja 3 valitse 3. Eli kaikki 4. rivin arvot. Joten meidän tarvitsee vain katsoa Pascalin kolmion 4. riviin ja sovittaa vastaukset.
4.rivillä on arvot: 1, 3, 3, 1. Joten minä vain korvata vastaukset meidän n valita K: n.,

Lopuksi, kaikki sinun täytyy tehdä on lisääntyvät ja yksinkertaistaa kunkin aikavälillä alas se on yksinkertaisin muoto. Älä unohda tarkistaa lopullinen vastaus varmista valtuudet kunkin termin vielä lisätä astetta alkuperäisen binomiaali! Luota minuun, se on uskomattoman helppo tehdä transkriptio virhe tämän tyyppinen ongelma 😉
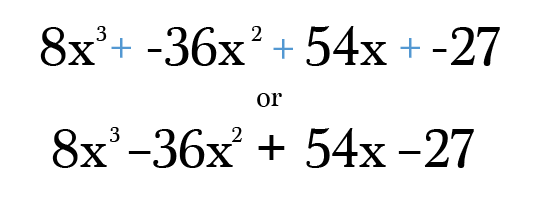
Tarvitsevat toinen esimerkki?,
yllä olevalla videolla näytän, miten Binomilausetta käytetään binomilauseen (x – 3Y)laajentamiseen. Lisäksi näytän sinulle joitakin ylimääräisiä temppuja pysyä järjestetty ja pari nopeaa tarkastuksia voit helposti tunnistaa yleisiä virheitä.
Kiitos lukemisesta!
❤ PYSYÄ YHTEYDESSÄ ❤
Pysy ajan tasalla kaikki Matematiikka Hakata on!