
Diracin delta-funktio on funktio, joka otettiin käyttöön vuonna 1930 P. A. M. Dirac hänen uraauurtava kirja, kvanttimekaniikka. Fysikaalinen malli, joka visualisoi deltafunktion, on äärellisen kokonaismassan m—integraalin massajakauma massajakauman yli., Kun jakautuminen tulee pienempi ja pienempi, kun taas M on vakio, massan jakautuminen kutistuu kohta massa, joka määritelmän on nolla määrin ja vielä on rajallinen-arvoltaan olennainen tasa-yhteensä massa M. raja, joka kohta massa jakelu tulee Diracin delta-funktio.
Heuristisesti, että Diracin delta-funktio voidaan nähdä jatkeena Kronecker delta integral indeksit (osat 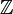 ) real indeksit (osat
) real indeksit (osat 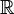 )., Huomaa, että Kronecker delta toimii ”filter” in summattu:
)., Huomaa, että Kronecker delta toimii ”filter” in summattu:
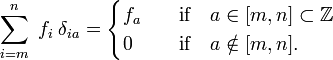
vastaavasti Diracin delta-funktio δ(x−a) on määritelty (korvaa i-x ja summa yli i: integrointi x),
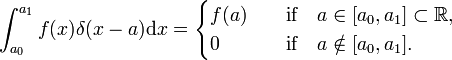
Diracin delta-funktio ei ole tavallinen hyvin käyttäytyviä map 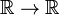 , mutta jakelu, joka tunnetaan myös nimellä sopimaton tai yleistynyt toiminto. Fyysikot ilmaisevat erityisluonteensa toteamalla, että Diracin deltafunktio on järkevä vain kokonaislukukertoimena (”integraalin alla”)., Matemaatikot sanovat, että Delta-funktio on lineaarinen funktio testifunktioiden avaruudessa.
, mutta jakelu, joka tunnetaan myös nimellä sopimaton tai yleistynyt toiminto. Fyysikot ilmaisevat erityisluonteensa toteamalla, että Diracin deltafunktio on järkevä vain kokonaislukukertoimena (”integraalin alla”)., Matemaatikot sanovat, että Delta-funktio on lineaarinen funktio testifunktioiden avaruudessa.
Sisällysluettelo
- 1 Ominaisuudet
- 2 Delta-convergent sekvenssit
- 2.1 Lohko toimintoja
- 2.2 Gaussin toiminnot
- 2.3 Lorentz-Cauchyn toiminnot
- 2.4 Sinc toiminnot
- 3 Johdannaiset delta toiminto
- 3.,1 Ominaisuudet johdannaisia
- 4 Primitiivinen
- 5 Diracin delta-funktio kolmiulotteisesti
- 6 Viitteet
Ominaisuudet
yleisimmin otetaan alempi ja ylempi sidottu määritelmä delta-funktio vastaa 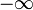 ja
ja 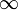 , vastaavasti. Tästä eteenpäin tämä tehdään.
, vastaavasti. Tästä eteenpäin tämä tehdään.
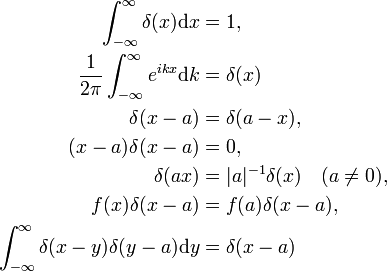
fyysikko on todiste nämä ominaisuudet etenee tekemällä oikea vaihdot osaksi kiinteä ja käyttää tavallisia sääntöjä integraalilaskennan calculus., Delta-funktio yksikköfunktion F(x) = 1 (toinen ominaisuus) Fourier-muunnoksena todistetaan jäljempänä. Viimeinen ominaisuus on analogisesti kertomalla kahden identiteetin matriisit,
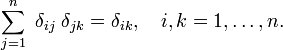
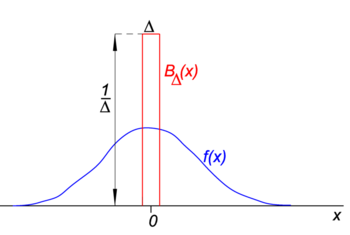
Kuvio. 1. Block (”boxcar”) funktio(punainen) kertaa säännöllinen funktio f (x) (sininen).
Delta-convergent sekvenssit
On olemassa perheitä säännöllisesti toimintoja, Fa(x), jonka perheen jäsenet eroavat arvon yksi parametri α., Esimerkki tällaisesta perhe on muodostettu perheen Gaussin funktiot Fa(x) = exp(−ax2), jossa eri arvoja yhden parametrin α erottaa eri jäsenet. Kun kaikki jäsenet ovat lineaarisesti normalizable, eli seuraava integraali on äärellinen, riippumatta siitä, α,
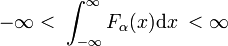
ja kaikki jäsenet huippu noin x = 0, niin perheen voi muodostaa delta-convergent järjestyksessä.,
Lohkon toiminnot
yksinkertaisin esimerkki delta-convergent sekvenssi on muodostettu perhe-lohkon toiminnot, jolle on ominaista positiivinen Δ,
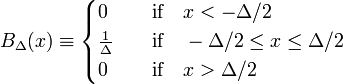
Kuvassa. 1 lohkofunktio BΔ näkyy punaisella. Ilmeisesti, alue (leveys kertaa korkeus) alla punainen käyrä on yhtä suuri yhtenäisyys, riippumatta siitä, mikä arvo Δ,
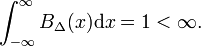
Anna mielivaltainen funktion f(x) (sininen Kuvio. 1) jatkuva (ei hyppyjä) ja rajallinen naapurustossa x=0., Kun Δ on hyvin pieni, ja lohko toiminto hyvin kapea (ja välttämättä ole kovin korkea, koska leveys kertaa korkeus on vakio) tuote f(x) BΔ(x) tulee hyvä lähentämisestä yhtä suuri kuin f(0) BΔ(x). Mitä kapeampi lohko,sitä parempi likiarvo., Siten Δ tulee nolla,
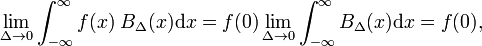
joka voi olla verrattuna määritelmä delta-funktio,
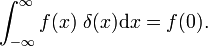
Tämä osoittaa, että perhe-lohkon toiminnot suppenee, että Diracin delta-funktio vähentää parametri Δ; perhe muodostaa delta-convergent järjestyksessä:
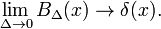
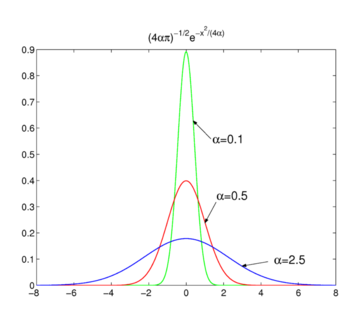
Kuvio. 2. Gaussin toiminnot.
huomaa: integroimme koko reaaliakselin., Ilmeisesti tämä ei ole välttämätöntä, emme voineet sulkea pois nolla-arvo siivet lohkon toiminto ja integroitu vain pahimman yli keskellä, alkaen −Δ/2 +Δ/2. Matemaattisissa teksteissä, kuten esimerkiksi Ref. , tämä hienosäätö integraatiorajoissa sisältyy delta-convergentin sekvenssin määritelmään. Toisin sanoen vaaditaan, että kahden siiven ylittävä integraali katoaa äärirajoilla. Koska Delta-convergent sekvenssit kohdataan fysikaalisissa sovelluksissa yleensä täyttävät tämän ehdon, jätämme tarkempi matemaattinen määritelmä.,
Gaussin toiminnot
Harkitse perhe,
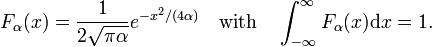
Kuten on esitetty Kuviossa. 2 funktioiden huippu on noin x = 0 ja suppenee α: n pienentämiseksi. Näin ollen perheen Gaussin toiminnot muodostaa delta-convergent järjestyksessä,
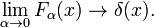
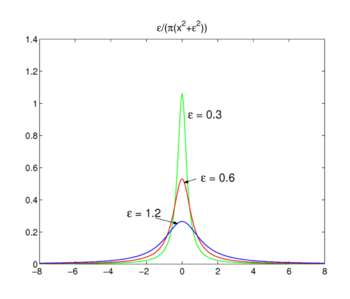
Kuvio. 3. Lorentz-Cauchyn toiminnot
Lorentz-Cauchyn toiminnot
perheen toiminnot on esitetty Kuviossa., 3
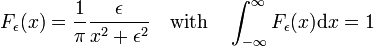
forms a delta-convergent sequence,
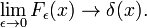
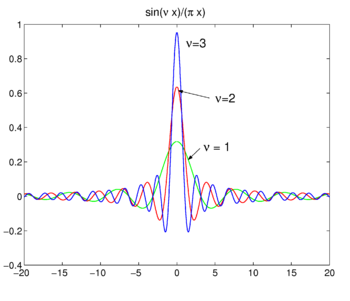
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 on,
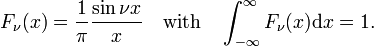
Tämän perheen suppenee delta-funktion lisäämiseksi v.
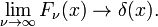
Tämä rajoitus johtaa helposti Fourier kiinteä edustus delta-funktio:
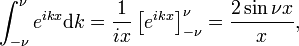
siten, että
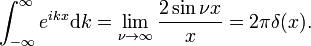
Diracin delta-funktio on Fourier-muunnos yksikön funktio f(x) = 1.
Johdannaisia delta-funktio
Harkitse derivoituva funktio f(x), joka häviää heti, plus ja miinus ääretön.,d=”ed7dae11d6″>
samalla tavalla kuin joku osoittaa, liikevaihto sääntö ja Hermiticity kvantti mekaaniset vauhtia operaattori 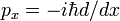 osoitimme täällä, että d/dx on anti-Hermitian,
osoitimme täällä, että d/dx on anti-Hermitian,
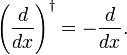
Todellakin, kun me kirjoittaa olennainen, koska sisäinen tuote, se seuraa osittainen integraatio ja vanishing f(x) integraation rajat, jotka
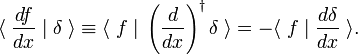
Tämä liikevaihto sääntöä käytetään määritelmää johdannaissopimuksen delta-funktio,
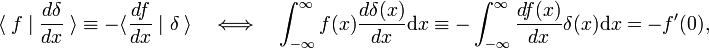
jos pääministeri ilmoittaa, ensimmäinen derivaatta f(x)., Deltafunktion määritelmän mukaan ensimmäinen derivaatta arvioidaan muodossa x = 0. Käyttämällä m-kertainen liikevaihto sääntö, se seuraa, että mth-johdannaisen delta-funktio on määritelty
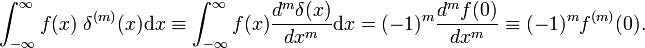
Ominaisuudet johdannainen
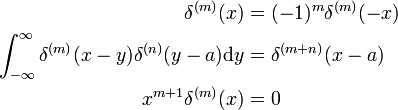
Nämä tulokset voidaan todistaa tekemällä korvaaminen x → −x ja käyttää liikevaihdosta sääntö d/dx (ks.edellä).,
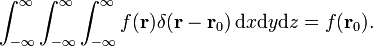
kolme-ulotteinen delta toiminto voidaan factorized
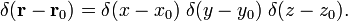
pyöreä polar koordinaatit
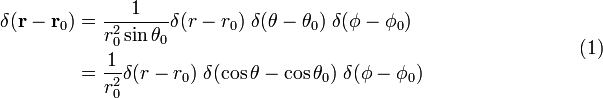
Todiste yhtälö (1)
Kirjoittaa
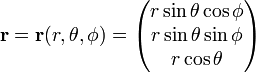
Jacobin matriisi (Jacobin determinantti) tämä muutos vuodesta Suorakulmaiset koordinaatit pallomainen polar koordinaatit on
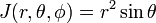
Harkita
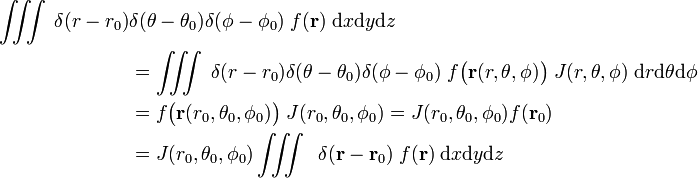
siten, että
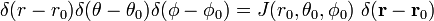
ja
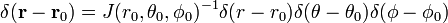
viimeinen rivi yhtälö (1) seuraa ketju sääntö.,
seuraavat hyödyllisiä ja usein sovellettu omaisuus on osoittautunut täällä,
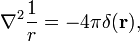
missä ∇2 on Laplacen operaattori kolmiulotteiset Suorakulmaiset koordinaatit ja r on pituus r.