Logaritminen toiminnot ovat käänteisesti eksponentiaalinen toimintoja. Eksponenttifunktion y = ax käänteisfunktio on x = ay. Logaritminen funktio y = logax määritellään eksponenttiyhtälöä x = ay vastaavaksi. y = logax vain seuraavin edellytyksin: x = ay, a > 0 ja≠1. Sitä kutsutaan logaritminen funktio, jossa pohja on.
Mieti, mitä käänteisen eksponenttifunktion tarkoittaa: x = ay., Kun otetaan huomioon luku x ja pohja a, mihin tehoon y on nostettava yhtä suuri x? Tämä tuntematon eksponentti, y, on logax. Logaritmi on siis vain eksponentti. Määritelmän mukaan alogax = x, jokaiselle todelliselle x > 0.
Alla ovat kuvaajat kuvassa muotoa y = logax, kun > 1, kun 0 < < 1. Huomaa, että domain koostuu vain positiivisia reaalilukuja, ja että funktio kasvaa aina, kun x kasvaa.,
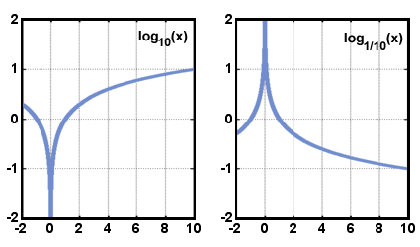
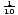 x.
x.verkkotunnus on logaritminen funktio on todellinen määrä suurempi kuin nolla, ja alue on todellinen määrä. Kuvaaja y = logax on symmetrinen kuvaaja y = ax suhteessa linjan y = x. Tämä suhde on totta mitään toimintoa ja sen käänteistä.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(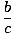 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
luonnollinen logaritmi-funktio on logaritminen funktio, jossa pohja e. f (x) = log e x = ln x, missä x > 0. ln x on vain uusi muoto merkintätapa logaritmi pohja e. Useimmat laskimet on painikkeita merkitty ”log” ja ”ln”. ”Loki” – painike olettaa, että pohja on kymmenen, ja” ln ” – painike tietenkin antaa pohjan olla e., Logaritmista funktiota, jossa on kanta 10, kutsutaan joskus yleiseksi logaritmiseksi funktioksi. Sitä käytetään laajalti, koska numerointijärjestelmässämme on base ten. Luonnollisia logaritmeja nähdään useammin laskuluvuissa.
on olemassa kaksi kaavaa, jotka mahdollistavat logaritmisen funktion pohjan muuttamisen. Ensimmäinen toteaa näin: logab = 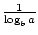 . Kuuluisampaa ja käyttökelpoisempaa kaavaa emästen muuttamiseen kutsutaan yleisesti peruskaavan muutokseksi. Sen avulla logaritmisen funktion pohja voidaan muuttaa mihin tahansa positiiviseen reaalilukuun ≠1. Sen mukaan logax =
. Kuuluisampaa ja käyttökelpoisempaa kaavaa emästen muuttamiseen kutsutaan yleisesti peruskaavan muutokseksi. Sen avulla logaritmisen funktion pohja voidaan muuttaa mihin tahansa positiiviseen reaalilukuun ≠1. Sen mukaan logax = 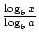 ., Tällöin a, b ja x ovat kaikki positiivisia reaalilukuja ja a, b≠1.
., Tällöin a, b ja x ovat kaikki positiivisia reaalilukuja ja a, b≠1.
seuraavassa jaksossa käsitellään joitakin eksponentiaalisten ja logaritmisten funktioiden sovelluksia.