Lunta yli pakkasessa | ScienceBits

oletko koskaan miettinyt, miten voi sataa lunta yli pakkasessa? Naiivi selitys on, että lumihiutaleiden sulaminen kestää vain aikaa, kun ne tunkeutuvat jäätyvän ilman yläpuolelle, kun ne laskeutuvat alaspäin maahan. Tämä on tietysti syy siihen, miksi rakeet voivat laskea lämpimässä säässä. Raekivet yksinkertaisesti putoavat nopeasti, liian nopeasti, jotta lämmin ilma sulattaisi rakeet. Tämä ei kuitenkaan ole pääselitys sille, miksi pakkasen yläpuolellakin voi sataa lunta.,
alla olevasta luvusta käy ilmi, että on selvää riippuvuutta kosteudesta – mitä kuivempi se on, sitä lämpimämpää voi olla lumisateen aikana. Tämä tarkoittaa, että tärkein tekijä, ainakin kuivissa olosuhteissa, liittyy kosteuteen. Ja tämä tekijä on haihtuminen. Tarkemmin sanottuna lumihiutaleiden laskeutuessa ne haihtuvat. Tämä prosessi kestää lämpöä ja pitää hiutaleet kylmänä.
näin ollen, jos haluamme laskea maksimilämpötilan, meidän on arvioitava hiutaleen nettolämpötasapaino. Ensinnäkin, kun hiutaleet kulkevat lämpimässä ympäristössä, ne saavat lämpöä ympäröivästä johtumisen kautta., Toiseksi lämpöä käytetään hiutaleiden haihduttamiseen, jolloin ne jäähtyvät. Jos haihtumislämpö ”pesuallas” on suurempi kuin lämmön johtuminen, hiutaleet pysyvät pakastettuina.
käy ilmi, että tämä on helppo laskea. Ei, se ei ole yksinkertainen laskea lämmön johtuminen tai haihtuminen lämpöä, mutta suhde on, koska erilaiset tuntemattomat geometriset tekijät peruuttaa.
jos laskutoimitus ei kiinnosta (koska et ole tiedefriikki), voit vain käydä laskurin sivulla.
Jos välität, tässä on derivointi., Oletetaan, että hiutaleiden ympärillä oleva virtaus on sellainen, että sen ympärille muodostuu leveyden d rajakerros. Yhteensä lämmön virtaus $F_H$ että hiutale (esim., J/s MKS) on antanut Fourier ’ s law:

$$ F_H \n {\kappa \over c} On {\Delta T \over c}, $$

missä $\kappa$ on lämmön diffuusiokerroin ilmassa (esim., m2/s MKS), c on lämpökapasiteetti ilmaa (J/kg MKS), A on pinta-ala rajakerros ympäri hiutale, kun ΔT on lämpötilaero hiutale ja ympäristö.,
Samoin, voidaan käyttää fickin laki saada diffuusio vesihöyryn pois hiutale (jossa lämpötila on lähellä jäädyttämistä, ja suhteellinen kosteus on 100%), ympäristöön, jossa lämpötila on korkeampi ja suhteellinen kosteus matalampi:

$$ \Phi_W \n D A {\Delta \rho_W \over c}. $$

Täällä, D on veden diffuusiokerroin (esim., m2/s MKS) ja ρ on veden höyry tiheys (kg/m3 MKS).,
haihduttamalla ice vaatii lämpöä, näin ollen, jos on vesihöyryn massa valovirta Φ päässä hiutale, se vaatisi lämpöä nopeudella $F_w = \epsilon \Phi$, missä $\epsilon$ on höyrystymislämpö jäätä (J/kg MKS).

korkein lämpötila, jonka yläpuolella lumihiutale sulaa, on lämpötila, jossa on kaksi lämmön virrat ovat yhtä:

$$ F_w = F_H ~~\oikea nuoli: ~ ~ \epsilon D \Delta {\rho_w \over c} A = {\kappa A \over c} {\Delta T_{max} \over c}.$$

Huomaa, että geometria virtauksen ympäri hiutale peruuttaa pois, koska sekä lämmön vuot riippuvat d ja samalla tavalla., Näin olisi myös, jos hiutaleen ympärillä oleva rajakerros on monimutkainen siten, että D todella riippuu suunnasta. Näin ollen

$$ \Delta T_{max} = c \epsilon {D \over \kappa} \Delta \rho = c \epsilon {D \over \kappa} \Delta (\rho_{la} RH).$ $

missä $\rho_ {La}$ on kylläisyyden vesihöyryn tiheys.
Kytkemällä numerot (joka löytyy esimerkiksi CRC handbook of chemistry and physics), tulokset implisiittinen yhtälö temperaturebecause kylläisyyttä vesihöyryn tiheys riippuu lämpötilasta sekä., Voimme yksinkertaistaa asioita, jos me sen sijaan kysyä, mikä on suhteellinen kosteus velvollinen pitämään hiutale jäädytetty tietyssä lämpötilassa. Se on:

$$ RH = 9.5 \exp \left(- 17.27 T_C \yli T_C + 238.3^\circ \right) \left( 10.5^\circ\mathrm{C} – T_C\right) \% .$ $

missä $t_c$ on lämpötila celsiusasteina.
tämä funktio on nähtävissä alla olevassa kuvassa yhdessä matsuon ja Sasyon tietojen kanssa vuodelta 1981. Kuten kuvasta näkyy, laskennallinen kuvaaja on suurin piirtein alaraja, jonka alapuolella ei ole lainkaan sadetta. Lämpimämmissä lämpötiloissa on sekoitus., Enimmillään noin 1°C ei-sulamisrajan yläpuolella on enimmäkseen lunta, kun taas noin 1-2°C rajan yläpuolella on enimmäkseen sadetta, mutta lumi on mahdollista. Nämä tapahtumat voivat johtua lisävaikutuksista, kuten voimakkaista alavireistä, lumen sulamiseen kuluvasta ajasta jne.

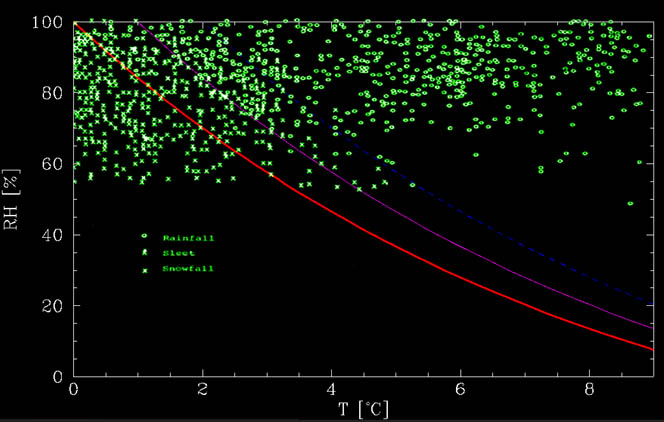
lumi vai sade? Punainen viiva on sulamaton viiva. Sen alla, lumi hiutaleet jäähdytetään haihduttamalla enemmän kuin ne lämpöä ympäristöstä ja siten pitää itsensä jäädytetty. Magneta-ja siniset viivat ovat +1°C ja +2°C no-sulamisviivan yläpuolella., Välillä 0°C ja +1°C yläpuolella ei sulata linja, se enimmäkseen lumet toteaa, että se enimmäkseen sateet välillä +1°C ja +2°C yläpuolella ei sulata line. Lämpimämmissä lämpötiloissa sataa. Vihreät datapisteet ovat Matsuon ja Sasyon (1981) keräämiä tapahtumia Wajimassa Japanissa vuosina 1975-1978.

näin ollen lämpimän sään lumitilanteita toivoessa tarvitaan erittäin kuivia olosuhteita. Esimerkiksi jos maanpinnan kosteus on vain noin 20% (hyvin harvinaista, koska jos on sadetta, ilmakehä on yleensä märkä!) sitten se voisi lunta 8°C (tai 46°F Englanti käyttäjille).,
Toinen vaatimus on, että missään pitkin laskeutua ei ilman ylittämään ei sulata line. Silloin hiutaleet tietysti sulavat.
Jos lämpötila nousee jäätymisen yläpuolelle, ei ole olemassa parametrejä, joilla Sademäärän tyyppi voidaan määrittää varmuudella. Silloin voidaan vain ennustaa, miten todennäköistä on, että lunta todella sataa. Tämä voidaan tehdä käyttämällä tulokset Häggmark ja Ivarsson (1997), vain korjattu käyttää jäädytetty-lamppu ja märkälämpötila.
pohjalukema on laskuri, jolla lumen todennäköisyys voidaan arvioida.,

miten se liittyy märkälämpötilaan? Suhde lämpötila löydämme ja jäädyttäminen veden lämpötila on hyvin samanlainen suhde kuiva-lamppu ja web-polttimo lämpötila (jos jälkimmäinen on alennettu lämpötila märkä lämpömittari lukee, koska veden haihtuminen). Tärkein ero on, että märkälämpötila sisältää veden haihtumista, kun taas meidän tapauksessamme, se on haihtuminen ice, 15% enemmän energiaa menetys. Näin, olemme pohjimmiltaan etsivät kuiva-polttimo lämpötila, jossa ”jäädytetty” lamppu lämpötila on 0°C.

Vastaa Peruuta vastaus